Next: PJ's Computational Model Up: No Title Previous: Introduction

Methodology

We employ a modified version of a spatial logic originally developed by Clementini et al. [6]. With respect to PJ our spatial logic deals with geometrical objects such as points, (directed) lines, convex regions, and text. It supports seven binary topological relations which may hold between these geometric objects. The objects and their possible relationships are defined using point-set theory (see [2] for definitions).

A major contribution of our approach is the mapping of our spatial logic to description logics theory and the application of this spatial description logic (DL) to semantics of visual languages. A DL is basically a term rewriting language restricting the left side of equations to single unique term names. There exist several theorem provers for special types of DLs. These theorem provers (referred to as DL systems) offer powerful reasoning mechanisms. They classify terms (also called concepts) by subsumption relationships between these terms. The DL systems automatically perform consistency checking (e.g. for incoherence, cycles) of term equations and offer retrieval facilities about the classification hierarchy. We refer to [7] and [8] for more information about DL theory and its applications.

We specify PJ's syntax and static semantics as predicates of our spatial logic. The predicates state necessary and sufficient conditions that have to hold between language elements. These formulae are defined as and consist of unary and binary predicates (representing concepts or spatial relations resp.) that can almost directly be translated to a DL. DL systems automatically recognize cyclic dependencies which usually result from recursive definitions. This is also true for the original, informal definition of PJ [3] that is somewhat ambiguous and context-sensitive.

  
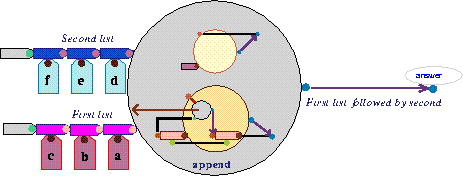
Figure 1: Append of two lists in Pictorial Janus