III. RESULT AND
DISCUSSION
The GA is used to evolve the weights
for the evaluation function used in the mini-max search by Ayo. Ayo was evolved
with a 3 and 5 level deep mini-max search.
A. Ayo with a
mini-max search of depth 3
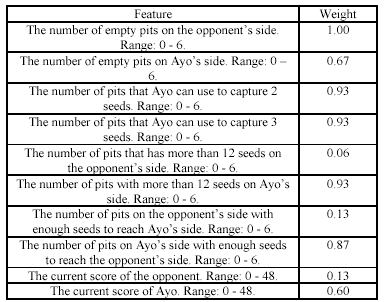
The values of the optimized weights
for a depth 3 mini-max search are listed in Table 1. This table indicates
that the number of empty pits on the opponent’s side has the highest weight of
all the features. This feature is the starting point for executing many
seed-capturing maneuvers and is indicative of Ayo’s ability to attack the
opponent in the future.
The number of empty pits on Ayo’s
side has a weight of 0.67. Ayo’s ability to defend itself is highly affected by
this feature.
The numbers of seeds that Ayo can
use to capture 2 or 3 seeds both have a weight of 0.93. This makes sense since
capturing seeds is the main aim of the game.
The number of pits with more than
twelve seeds, a feature of relevance to the kroo strategy has a
weight of 0.93.
The number of pits with enough seeds
to reach the other side is given a weight of 0.87. This feature is very
important because it assists Ayo identifying its offensive strength.
The evaluation function employed by
Ayo consists of other features such as the scores of both players at each
instant. Ayo’s score was given a higher weight (0.6) than its opponent’s score
(0.13).
Finally, the numbers of pits that
the opponent can use to capture 2 or 3 seeds are assigned 0.67 and 0.20 weights
respectively. Both features affect Ayo’s ability to be defeated and reflects its
bias towards attack rather than defense.
TABLE 1
The Weights of The Features in The Evaluation Function as Generated by The
GA for Mini-Max Search of Depth 3

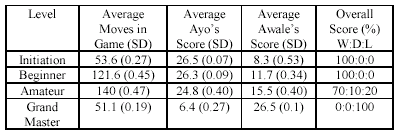
To evaluate the performance of Ayo,
Ayo played 10 games at each level of the four levels of “Awale”. The results are
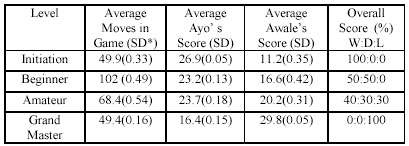
presented in table 2.
Awale won all the games at the
initiation level; at the beginner level Ayo won 5 of the 10 games and drew the
remaining 5 games. Ayo portrays its ability to use Kroo moves by turning
around 3 games to win them at the amateur level; it won 4, drew 3 and lost 3
games. Ayo was not able to win any game at the grand master level but it was
able to capture a decent average of 16 seeds in the 10 games.
Davis et al. [5] developed an
evaluation function that focuses on the number of seeds that could be captured
by both players and their score. Their results (against Awale) are shown in
table 3 below.
Comparing the results of Davis et
al. (table 3) to Ayo’s results, shows that the enhancement of the evaluation
function makes up for the low search depth of Ayo.
TABLE 2
Ayo’s Results for Mini-Max Search of Depth of 3
*SD stands for Standard
Deviation
TABLE 3
Result of Davis et al. for Mini-Max Search of Depth of 7
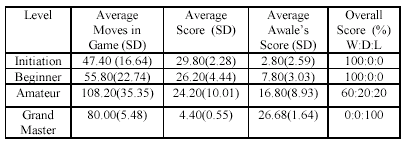
Table 2 and 3 show very little
difference in the result between Daviset et al. depth 7 mini-max search
and Ayo depth 3 mini-max search. The results at other levels exhibit the same
similarity in terms of average scores. The most significant result is that of
the grand master level, where Davis et al. player captured an average of
4.40 seeds, while Ayo captured 16.4 seeds, on average.
B. Ayo with a
Mini-max search of depth 5
The result of the Ayo player with
depth of 5 is depicted in the table 5, where table 4 contains the list of values
of the weights used to achive the results in table 5. The results depicted in
table 5 show improvements in the number of wins per level. dd
At the initiation level, Ayo won all
the games. At the beginner level, Ayo won all the games. At the amateur level,
Ayo won seven games (10% more than Davis’ et al. player), drew one
and lost one game. Finally, at the grand master level, Ayo lost all the games
(but still managed to return a higher score than Davis’ et al. player).
Hence, what is significant is that, in comparison to Davis et al. player
(with 7 levels of search depth), Ayo with 5 levels of search depth, still
managed to win more games and collect more points.
I. CONCLUSIONS
& Recommendations
Problem solving is one of the main
purposes of Artificial Intelligence research. Prolem Solving consists of two
sub-processes: choosing an apropriate representation and performing a search.
Knowledge representation should include analysis, conceptualization and
formalization. A good knowledge representation may considerably reduce the
amount of search needed to solve a problem, while a poor representation may
render solving the problem impossible. Therefore, choosing a representation
should have a high priority in problem solving [10].
TABLE 4
The Weights of The Features in The Evaluation Function as Generated by The
GA for Mini-Max Search of Depth 5
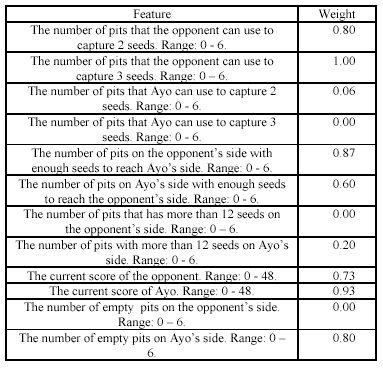
TABLE 5
Ayo’s Results for Mini-Max Search of Depth of 5
In this paper, we illustrate the importance of problem domain representation,
using our own Awali playing program: Ayo. We use a Genetic Algorithm to
optimize the weights of the feature evaluation function of Ayo. We play Ayo
against a commercially available Awari player, then compare Ayo’s results to the
results achieved by an older Awali player; one that uses a 7-levels deep
mini-max search. Ayo, with a 5-levels deep mini-max search, returns better
results, due to better more intelligent representation of the state space.
Game-players that execute shallower
searches require less resources and run faster than game-players that require
deeper searches. Hence, it should be possible, in principle, to speed-up many
two-player endgames, such as chess and checkers by including better more
intelligent features of the current state of the game, rather than executing
ever deeper searches of future moves trees. After all, the best chess players in
the world have very limited search capabilities compared to even the humble PC!
REFERENCES
[1] The
university of Alberta computer Awari Group, http://www.cs.ualberta .ca/~awari/.
[2] V. Allis, M. van der Muellen, and J. van den Herik,
"Proof-number Search", Artificial Intelligence, vol. 66, pp.91-124, 1994.
[3] J. Van der Rijswijck, "Learning from Perfection: A Data
Mining Approach to Evaluation Function Learning in Awari". In proceedings
of the 2nd International Conference (CG-00), Hamamatsu, vol. 2063,
pp.115-132, 2001.
[4] J. W. Romein and H. E. Bal, "Awari is Solved". Journal of
the International Computer Games Association (ICGA), vol. 25, pp.162-165,
2002.
[5] J. E. Davis and G. Kendall, "An Investigation, using
Co-Evolution, to evolve an Awari Player". In proceedings of Congress on
Evolutionary Computation (CEC2002), Hawaii, pp.1408-1413, 2002.
[6] C.R. Darwin, The Origin of Species, Vol.11, Ch. 4,
P.F. Collier & Son, New York, 1909.
[7] J. Cogleyd, "Designing, implementing and optimizing an
object-oriented chess system using a genetic algorithm in Java and its critical
evaluation ", M.S thesis, The Open University, London, England, 2001.
[8] A. S.
Fraenkel, "Combinatorial Games: Selected Bibliography with a Succinct Gourmet
Introduction", Games of No Chance, vol. 29, MSRI Publications, Cambridge
University Press, pp.493-537, 1996.
[9] M. Page-Jones, Fundamentals of Object-Oriented Design in
UML, pp. 13,33 Dorset House Publishing, New York, 2000.
[10] S. Russell and P. Norvig, Artificial Intelligence,
New Jersey: Prentice Hall, Ch. 3-5, pp.55-149, 1995.
[11] P. S. Wang, Standard C++ with Object-Oriented
Programming, Pacific Grove: Kent State University, 2001.
[12] Awari Statistics, http://awari.cs.vu.nl/statistics.html.
[13] The rules of Awari, http://www.cs.ualberta.ca/~awari/
rules.html.
[14] Awari-a game from Africa, http://www.guidezone.skl.com/
liz_africa_games.htm.
[15] computer Olympiad 2000-Awari, http://www.dcs.qmul.ac.uk/ ~olympiad/awariresult.htm.
[16] Oware by many other names, http://www.svn.net/rkovach/
oware/owarname.htm.
[17] Thomas R. Lincke, Strategies for the Automatic Construction
of Opening Books: Computers and Games 2000: 74-86.
[18] Mind sport Olympiad, Lonndon, 2000, http://www.msoworld.com/
history2000/jpg/c-comput.htm.
Page 1,
Page 2 |