|
INTRODUCTION AND REVIEW
A. Introduction
The performance of a GA is dependant on a
number of factors, including candidate solution representation, and fitness
evaluation and genetic manipulation. Both crossover and mutation have
parameters (probability of crossover Pc and probability of mutation Pm) that
require initialization and adjustment. For a given problem, these parameters,
as well as the size of the population of candidate solutions (S), require
careful manual optimization, often done through trial and error. Naturally,
this diminishes the autonomy of GAs, and renders them much less attractive to
potential users, such as engineers, that are not experts in GAs. Parameterless
GAs (pGAs) represent an attempt (not yet complete or widely used) to eliminate
the need for manual tuning of GA parameters.
In this paper we provide an overview of the
various types of pGAs, and present the results of an empirical comparative
study of five different pGAs.
B. Review
There are two main approaches to the
elimination of parameters in GAs: a) Parameter Tuning, and b) Parameter
Control. Parameter tuning involves finding good values for the parameters
before the GA is run and then using these values during the GA run. In
Parameter Control, one starts with certain initial parameter values; possibly
the De Jong [8] or Grefenstette's [11] sets or some amalgamation thereof. These
initial values are then adjusted, during run-time, in a number of ways. The
manner in which the values of the parameters are adapted at run-time is the
basis of Eiben's classification of Parameter Control into three different
sub-categories (Eiben et al. [9]). These sub-categories are: a) Deterministic,
b) Adaptive and finally c) Self-adaptive. A brief review of published work in
these three areas of Parameterless GAs follows.
Deterministic Paramterless GAs
. In this type of Parameterless GAs, the values of the
parameters are changed, during a run, according to a heuristic formula, which
usually depends on time (i.e. number of generations or fitness evaluations).
Fogarty et al. [10] alter probability mutation in line with equation (1)- t is
the generation number.

Hesser et al. [13] derived a general formula for
probability of mutation using the current generation number, in addition to a
number of constants (and ) used to customize the formula for different
optimization problems. Unfortunately, these constants are hard to compute for
some optimization problems. In equation (2) n is the population size, l
is the length of a chromosome (in bits), and t is the index of the
current generation. , , 2 1 C C 3 C
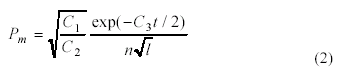
Both Back [3] and Muhlenbein [15] discovered, experimentally,
that 1/l (where l is chromosome length) is the best value for Pm
for (1+1) GAs. A (1+1) GA is an algorithm that sees single parent
chromosomes each producing a single child by means of mutation. Hence, the best
of parent and child is passed to the next generation. In other studies [4],
Back proposes a general formula for Pm, one that is a function of both
generation number (t) and chromosome length (l). The formula is
presented as equation (3); T is the maximum number of generations
allowed in a GA run.
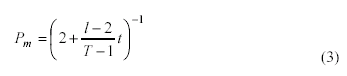
All formulae presented
above are variations on a single theme presented symbolically by 1/t,
where t is the generation number. In this theme the probability of
mutation is initially very high, but is quickly reduced to a low and reasonably
stable value. This agrees with common sense, as most GAs go through a short and
frantic period of locating areas of interest on the fitness surface, followed
by a lengthy and deliberate exploration of those locales (mainly via crossover).
Naturally, random search (and hence mutation)
are ineffective methods of exploration of large spaces. This simple fact leads
to the incorporation of 1/l (and variants) into many formulae for Pm
- l is the length of the chromosome, which is linked to the
dimensionality of the search space. Not only is the need for manual tuning of Pm
eliminated, but the performance of GAs is much improved by the use of
time-dependant formulae for Pm. This conclusion is supported by many
studies, including [5].
Adaptive Paramterless GAs
. In this mode of parameter control, information fed-back
from the GA is used to adjust the values of the GA parameters, during runtime.
However, (as opposed to self-adaptive control) these parameters have the same
values for all individuals in the population.
Adaptive control was first used by Rechenberg
[16]. He asserted that 1 every 5 mutations should lead to fitter individuals.
As such, he enforced a variable mutation probability that was controlled by the
rate of successful mutations in a population. If, at one point in time, the
fraction of successful mutations was more than 1/5 then the probability of
mutation is decreased and visa versa. Similarly, Bryant et al. [7] increased or
decreased the probabilities of crossover and mutation (from initial values) as
a function of how much or little those probabilities contributed to the
generation of new fitter individuals in a given population: an elaborate credit
allocation system was employed, and is detailed in their paper.
Schlierkamp et al. [17] focused their efforts
on adapting the size of the population. Indeed, they simultaneously evolved a
number of populations with different sizes. After each generation, the
population with the best maximum fitness is stored in a quality record. After a
number of generations, the population with the highest record is increased; all
other populations are decreased. In similar fashion, Hinterding et al. [14] ran
three populations simultaneously. These populations had an initial size ratio
of 1:2:4. After a certain pre-specified time interval the populations are
halved doubled, or maintained as is, depending on the relative fitness values
of their fittest individuals. Along the same theme, Harik et al. [12] ran races
between multiple populations of different sizes, allocating more time to those
populations with higher maximum fitness, and firing new populations whenever
older populations had drifted towards suboptimal (search) subspaces.
On a different note, Annunziato et al. [2]
asserted that an individual's environment contains useful information that
could be used as a basis for parameter tuning. They used a trip-partite scheme
in which a new parameter (meeting probability) influences the likelihood of
meeting between any two individuals, which (if they meet) can either mate or
fight.
Self-adaptive Paramterless GAs
. These GAs use parameter control methods that utilize
information fed back from the GA, during its run, to adjust the values of
parameters attached to each and every individual in the population. It was
first used by Schwefel [18] in an Evolutionary Strategy (similar to a GA, but
using real numbers and matching operators, instead of bit strings, for
chromosomes), where he tried to control the mutation step size. Each chromosome
in the population is combined with its own mutation variance, and this mutation
variance is subjected to mutation and crossover (as is the rest of the
chromosome). Back [6] extended Schwefel's [18] work to GAs. He added extra bits
at the end of each chromosome to hold values for the mutation and crossover
probabilities. At first, the mutation and crossover probability values were
chosen at random. Then, these bits were subjected to the processes of evolution
until, gradually, chromosomes with better probabilities appeared, and hence
dominated the population. Another way of self-adapting GA parameters, described
by Srinivas et al. [19], involves assigning mutation and crossover
probabilities to each chromosome, based on its own current fitness and the
fitness of the population at large. Arabas et al. [1] defined a new remaining
life time (or RLT) variable, which is attached to every chromosome and is used
to determine whether it will survive or not.
TEST ALGORITHMS AND TEST FUNCTIONS
A. Test Algorithms
The test algorithms are: a) Traditional
Steady-State Genetic Algorithm (TSSGA). This algorithm is not a true
parameterless GA, but we make as one by fixing the values of its parameters,
without any preparatory tuning via trial and error. It comes from Back et al.
[12]; b) Self-Adaptive Mutation Crossover and Population Size for Genetic
Algorithms (SAMXPGA). This GA also comes from Back et al. [12]; c) Adaptive
Evolutionary Algorithm via Reproduction and Competition (AEARC). This GA comes
from Annunziato et al. [3]; d) Adaptive Population Size Genetic Algorithm
(APSGA). This GA comes from Harik et al. [23]; and e) Deterministic Intelligent
Mutation Rate Control Canonical Genetic Algorithm (DIMCCGA). This GA comes from
Back et al. [9].
B. Test Functions
To evaluate the performance of the five
Parameterless GAs, we use the same test functions used in [12] - we restate
them here for convenience. This set of test functions have a) problems
resistant to hill-climbing; b) nonlinear non-separable problems; c) scalable
functions; d) a canonical form; e) a few uni-modal functions; f) a few
multi-modal functions of different complexity with many local optima; g)
multi-modal functions with irregularly arranged local optima; h)
high-dimensional functions. All test functions have 10 dimensions and use 20
bits/variable except for f5, which uses 6 bits/variable.
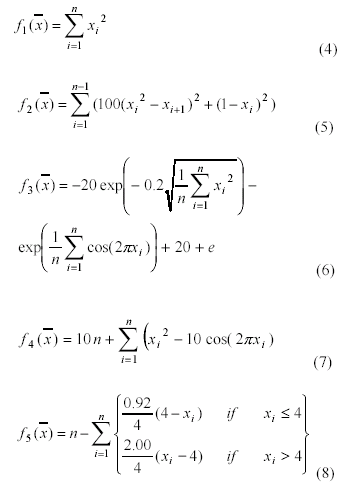
Page 1, Page 2,
Page 3
|

![]()
