

Next: GenEd Up: No Title Previous: Motivation and Introduction


Next: GenEd
Up: No Title
Previous: Motivation and
Introduction
We believe that the semantics of formalisms used for VL theory should be well understood. That is, the meanings of represented language concepts should be unambiguously determined by explicit notational formalisms, so that algorithms can operate on the representation in accordance with the semantics of the notation, without needing ad hoc provisions for specific VL domains. Our approach is based on a fully formalized theory [4] for describing visual notations that consists of three components. Each component is defined by precise semantics. Objects and relations are defined by point-sets and topology. Description logic theory can be based on model-theoretic semantics using a compositional axiomatization with set theory.
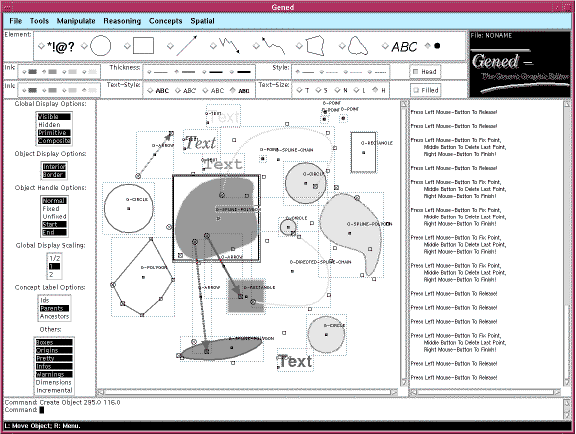
Figure 1: Examples for geometric objects (full image).
GenEd implements these three components in accordance to our theory. However, the implementation of geometrical objects and their corresponding spatial relations uses well-known computer graphics techniques for reasons of efficiency. The semantics of these algorithms are still specified within our theory (see [5] for a complete treatment). GenEd offers a set of predefined geometrical objects (similar to other object-oriented graphic editors) that can be used to design examples of particular notations. Supported primitive objects are points, (directed) line segments, line segment chains, and (spline) polygons (see Figure 1).
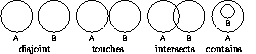
Figure 2: Primitive relations between A and B

Figure 3: Higher-level relations
GenEd recognizes seven primitive spatial relations (disjoint, touches, intersects, contains_by, covers_by ) that may hold between two objects (see Figure 2). It also computes the dimension of the intersection, if applicable. The semantics are defined in analogy to a proposal by Clementini et al. [6] and are based on point-sets and topology. The relations have a parameterized `fuzziness' compensating for inexact positioning of objects (caused by users or scaling factors) and floating-point arithmetic. In contrast to several other approaches for spatial relations (e.g. see [4]) GenEd can also deal with concave objects. Additionally, an arbitrary collection of objects may be grouped together and treated as a composition object. Analogous semantics for composition objects were defined.
Higher-level relations can be defined with the help of the above mentioned seven relations (see Figure 3). GenEd currently recognizes specialized containment (directly-contains), connectivity (linked-with), and direction of line segments (starting-from, pointing-to). These relations are also applicable to composition objects.
Description logic (DL) theory has been successfully applied to the specification of Pictorial Janus (PJ) [2,3], a completely visual language for concurrent logic programming [1,7].
DL theories are based on the ideas of structured inheritance networks [8]. A DL can be considered as a term rewriting language restricting the left side of equations to single unique term names. The specification of a DL consists of a set of concepts (or terms), a set of roles (binary relations that may hold between individuals of concepts), a set of disjointness assertions among concepts and among roles, a set of concept membership assertions for individuals, and a terminology, which maps names to specifications of concepts or roles. Concepts may be primitive or defined . A specification of a primitive concept represents conditions that are necessary but not sufficient. The specification of a defined concept represents conditions that are both necessary and sufficient. Primitive and defined roles are similarly specified. If a role holds between individuals, these individuals are referred to as fillers of this role. The meaning of DL theory can be described by model-theoretic semantics using a compositional axiomatization with set theory. The appendix summarizes the semantics of DL language elements that are used in the following sections.
There exist several theorem provers for special types of DLs. These theorem provers (referred to as DL systems) offer powerful reasoning mechanisms that are based on the DL semantics. DL systems usually distinguish two separate reasoning components. The terminological reasoner or classifier (TBox) classifies concepts with respect to subsumption relationships between these concepts and organizes them into a taxonomy. The TBox language is designed to facilitate the construction of concept expressions describing classes (types) of individuals. The classifier automatically performs consistency checking (e.g. for incoherence, cycles) of concept definitions and offers retrieval facilities about the classification hierarchy. The forward-chaining assertional reasoner or realizer (ABox) recognizes and maintains the type (concept membership) of individuals. The purpose of the ABox language is to state constraints or facts (usually restricted to unary or binary predications) that apply to a particular domain or world. Assertional reasoners support a query language as access to their state. Some query languages offer the expressiveness of the full first-order calculus.
GenEd defines several predefined primitive concepts resembling supported
geometric objects. It also introduces a set of primitive roles representing
the spatial relations described in the previous section. The built-in spatial
parser of GenEd can recognize these objects and their spatial relationships.
GenEd can create for elements of a drawing a corresponding set of ABox elements
asserting concept membership (e.g. geometric object
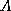 is a rectangle) and role fillers
(e.g. rectangle
is a rectangle) and role fillers
(e.g. rectangle 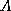 touches line
touches line
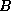 ). GenEd's roles are organized in
a hierarchy with inheritance for role fillers. Roles with at most one filler
are referred to as attributes (e.g. text_value for text elements).
Many geometric attributes are available for objects (size, position, ink, etc).
GenEd also maintains part-of relationships for composition objects.
). GenEd's roles are organized in
a hierarchy with inheritance for role fillers. Roles with at most one filler
are referred to as attributes (e.g. text_value for text elements).
Many geometric attributes are available for objects (size, position, ink, etc).
GenEd also maintains part-of relationships for composition objects.


Next: GenEd
Up: No Title
Previous: Motivation and
Introduction