|
1 Introduction
1.1 The Approach
It is very tempting to describe computer simulations using
everyday words. For example: simulated agents are said to 'move', 'eat',
'trade', 'fight', and 'reproduce'; simulated birds ('boids') are said to
'flock'; and so on.
The danger of this practice is that we may be easily misled
into believing that we are actually simulating the named activity, with the
result that we read more into a computer simulation than is actually happening
there.
To avoid this problem, we intend to use extremely precise
terminology. This does not necessarily preclude the use of common words, but we
will use those words only after describing very precisely what they mean in the
simulation.
As an example, suppose we say that an agent 'eats'. Perhaps
one of the things that a viable agent has to do in the simulation is to maintain
a string of characters (where 'character' is one of "a", "b", etc.). If the
string becomes empty, or contains useless characters, the agent dies. In this
context, we might define 'eat' as 'transfer one or more characters from the
environment to the internal character string'.
Our usage is like that of mathematics. In mathematics, saying
'relation' does not produce an image of one's grandmother and saying 'field'
does not lead to thoughts of grazing cows (or should not). To avoid the problems
of anthropomorphism in Artificial Life (AL) studies, we propose Formal
Artificial Life or FormAL for short. To motivate this decision, we
review Formal Logic.
The original purpose of logic was to model the processes of
human reasoning. However, formal logic does not do this. It is a symbol
manipulation system with various possible interpretations and, in many cases,
the intended interpretation is to reason about a particular model. As an
example, consider the theorem of propositional calculus (also an axiom in some
variants):  .This
is a purely symbolic statement. In a particular application, we might choose the
following interpretations of the propositions:
 the
shape has three sides
 the
shape is a triangle
and interpret the theorem as saying "since my shape has three
sides, and a shape with three sides is a triangle, I infer that my shape is a
triangle". But the symbols can equally well be interpreted as
 the moon is blue
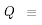 the coffee is
cold
giving "since the moon is blue, and blue moons imply cold
coffee, I infer that my coffee is cold" which does not provide a typical example
of human reasoning.
Researchers in AL write simple programs and provide
explanations of the form "when an organism sees food, it eats, and when it sees
another agent that is suitably sexy, it falls in love and reproduces". But this
is only one possible interpretation of a few changing numbers.
Of course, these statements open possibilities for
philosophical discussion. We could say that what animals really do is transform
one bunch of proteins into another bunch of proteins and observers interpret
this activity as "eating". However, the basic point that we are trying to make
here is that biological activities, such as eating, are generally rather
complex, whereas the activities in AL simulations are, by comparison, rather
simple.
In FormAL, we provide a precise description of the algorithm
that we use, and an intended interpretation that explains why we believe that
the algorithm might contribute to the theory and practice of AL.
As another way of ensuring precision, we make a careful
distinction between laws and life. The unchangeable
operation of the simulated universe is defined by laws; the changeable processes
that may occur within the universe constitute life.
As an example, many evolutionary programs replicate the
fittest individuals. Thus fitness and replication are "laws", because they are
determined by the environment - the agents have no influence over them. We
prefer to make fitness and replication part of "life", meaning that the agents
can choose how to evaluate their fitness and have a mechanism for reproducing
that can evolve. Capabilities such as these are called self-adaptation.
Blocks of text with this format (indented and italic) suggest
possible interpretations of the formalisms introduced in §4.
1.2 Overview
This paper outlines a plan for a simulation of interacting
agents. The primary goals of the project are:
. to determine a set (or sets) of conditions in which complex
"artificial life" can evolve from simple starting conditions;
. to develop a programming language that is well-suited to
the description of evolving agents.
Our expectation that complexity can evolve under suitable
conditions is based on the following argument (due to Stephen Jay Gould). In
Figure 1, organisms are represented as small circles in a space in which
complexity increases to the right. Each organism can give birth to new organisms
that are close to it in this space. At the left of the diagram there is a
barrier: an organism on the left of this barrier would be too simple to survive.
Assuming that organisms continue to multiply and diversify, the distribution of
complexity will change: it is bounded on the left, but its rightmost point will
drift further to the right. This is not because evolution is goal-directed
(seeking greater complexity) but is a simple consequence of bounded random
change.
Figure 1: Evolving
complexity
Gould's view may be contrasted with StephenWolfram's view.
Wolfram believes that complexity is an emergent property of simple mechanisms
and the evolution is unimportant in the development of complexity and, in fact,
has a tendency to simplify. Wolfram demonstrates that simple machines (cellular
automata or CA) can exhibit complex behaviour. The truth probably lies somewhere
in between Gould's view (evolution leads to complexity) and Wolfram's view
(evolution leads to simplicity): both the emergent behaviour of simple
mechanisms and the ability of a population of variant individuals
are needed for interesting results.
Evolution will tend to select the simplest mechanism that
provides suciently complex behaviour. But simple mechanisms may not exist for
certain tasks, and complex - often over-complex and redundant - mechanisms will
evolve for these tasks. One of the goals of our research is to investigate the
relative importance of Gouldian evolution and Wolframian emergence.
Despite Wolfram's claims, CA are not simple, at least in a
biological sense. Wolfram chooses simple initial conditions (typically
...000010000...., where "...." denotes an infitine string of "0"s) but, after
n steps of processing, the active string may be as long as 2n
characters. The amount of work required to simulate a CA increases linearly with
time, and is therefore unbounded.
A natural organism is a finite-state machine: although the
number of states may be very large, it does not increase indefinitely.
One way of evolving complexity would be to employ a measure
of complexity as a fitness function. This would defeat the purpose of our
experiment, which is to observe complexity as an emergent property of a
system. Complexity should be a part of "life", not a "law".
The project is motivated by the observation that many early
experiments in evolutionary programming (EP) ignore significant aspects of
biological evolution. This is not necessarily a bad thing, because the
experiments often achieve their goals - for example, to find optimal values of a
set of parameters in a large search space. The limitation of these experiments
is that the systems are restricted to finding values for the parameters: they
cannot, by design, find alternative solutions. To be fair, there have also been
recent studies that include self-adaptation.
The biological aspects that we plan to incorporate are some
or all of the following. An "organism" is a biological organism such as an
aardvark or a zooplankter.
. Much EP work focuses on optimization, implying that there
is an optimum fitness or "best genome". In contrast, biological systems maintain
large populations of organisms, providing a continuously changing gene pool and
the ability to adapt.
. All but the simplest organisms (phages) contain
reproductive machinery to build copies of themselves. This distinguishes them
from EP, in which replication is performed by "magic" (that is, the controlling
software). Tom Ray's Tierra (and other so-called autoadaptive systems)
are the exceptions.
. Consequently, the biological phenotype is not fully
determined by the genotype, because the form of the newborn organism depends on
the reproductive environment as well as the genome.
. The structure of the genome can evolve.
. The genetic code can evolve.
. The genome is not a complete description of the organism.
You can't make a dinosaur from dinosaur genes: you need a female dinosaur, too.
. The genome of an organism affects the entire life of the
organism, not just its form at birth. Consider, for example, the fact that
genetic diseases may appear for the first time late in life. Each cell uses its
copy of the genome continuously, enabling the genes that synthesize the proteins
that it needs and disabling the others.
. Most genes do not code for a single characteristic.
Changing a single gene may have several effects, and the effects can be good or
bad. Here is the classical example (simplified): if you have the homozygous form
of the sickle-cell gene (that is, two copies of the same allele), bad luck - you
will die of anemia; but if you have the heterozygous form (one copy), you are
resistant to malaria. Consequently, the frequency of the sickle-cell mutation in
the population depends on the likelihood of catching malaria.
. The genome plays a dual role. It is treated as data
when it is copied from parent to child. It is treated as instruction when
it is used to build or maintain the organism.
The current proposal can be summarized as follows:
Primary Goal: To study the emergence of complexity.
Principle: It is pointless to include a variable in an
agent unless the variable is genetically controlled (or, at least, genetically
influenced).
Out of sheer necessity, some factors must be statically
included as "hardwired" attributes.
For example, we explain below how the value of food to an
agent depends on both the kind of food and a parameter of the agent. This
implies that the parameter must be genetically controlled so that agents can
evolve to maximize the benefit of feeding.
Means:
1. An agent is a simulated organism.
2. Design an agent that is as simple as possible while being
able to:
. reproduce itself using genetic information;
. modify the structure of the genome between generations;
. interact with other agents;
. survive and reproduce in a challenging environment.
3. Simulate a population of agents.
Figure 2 shows approximate links from agents (on the left) to
organisms (on the right).
Figure 2:
Page 1,
Page 2, Page 3,
Page 4, Page 5
DEC Lab Home
Last Updated April 6, 2004
|