|
2 Laws
As explained in §1, our approach distinguishes "laws", which
are properties built into the computer simulation that cannot be changed by
agents, and "life", which is the adaptive part. In this section, we propose some
laws.
Here is an ideal experiment: encode the physical and chemical
properties of atoms and simulate the behaviour of a number of atoms interacting
over a period of time.
Since the ideal experiment is impractical, we must start at a
higher level than the physical and chemical properties of atoms.
Comparison of the 'goal' and the 'ideal experiment' indicates
that we have to find an interesting intermediate region between two extremes: if
we hypothesize too little, the experiments take too long; if we hypothesize too
much, we simply observe the behaviour we have programmed.
2.1 Constants
A universal constant is a number that is fixed
(at least for one simulation).
2.2 Space
Agents move in a space. Possibilities for modelling the space
include:
. Continuous: En
(n-dimensional Euclidean space).
Realistic but may be computationally expensive.
. Discrete:
- N n
(n-dimensional discrete space, e.g.,
chessboard, where N is the set of natural numbers). Easy to visualize.
- 2n (n-dimensional hypercube). E�cient to
compute.
. In the simplest case, the space is a well-mixed soup in
which agents interact at random but the simulation does not need to record their
exact position. This approach precludes any adaptation to the space. Movement is
meaningless because it has no effect on the rate of interaction with other
agents. Spatial phenomena are efectively removed from the simulation.
. In a realistic model, agents would move in 3D Euclidean
space. The computational cost is probably excessive.
. In a simplified model, agents move on a square grid (like a
chessboard - N2). Each cell of the grid has 4 neighbours (8 if we include
diagonals). Edge e
ects can be avoided by joining opposite sides to create a torus.
. As a compromise, agents could move in
En but
adjacency could be approximated in Nn.
. Another approach would be to use Hamming distance. A
position is represented by a string of bits and the distance between two
positions is the number of bits at which they differ (that is, the number of
zero bits in the exclusive-or of the positions). Example: 8 bits give 256
positions. Advantage: fast to compute. Disadvantage: not very intuitive.
Current Choice: The space currently chosen for the
simulation is described below.
Space is a three-dimensional lattice of discrete points. Let
 be the set { 0,
1, . . . , S - 1 } where the universal constant S is a small
positive integer such as 10 or 20. Then each point in space has a
coordinate of the form be the set { 0,
1, . . . , S - 1 } where the universal constant S is a small
positive integer such as 10 or 20. Then each point in space has a
coordinate of the form
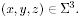
Arithmetic in space is performed modulo S: the result
of any arithmetic operation on coordinates is a member of
 . (This is the
topology of a torus in four dimensions.) . (This is the
topology of a torus in four dimensions.)
The distance between two points p1 = (x1, y1,
z1) and p2 = (x2, y2, z2) is defined by the
"Manhattan metric". There are two ways of getting from one lattice point to
another one on the same axis, and we always choose the shortest way. The maximum
possible distance between two points in one dimension is S/2 and, in
general, the distance between points p1 and p2 is given by

Figure 3 shows the distances between lattice points in a
single dimension in a space with S = 10. The discreteness of space
enables e�cient simulation. In particular, it avoids problems such as computing
the distances between all pairs of agents (which takes time (N2) for N
agents). Visualization of the simulation may use continuous space. For
example, agents may move with arbitrary speed in arbitrary directions but, as
far as the "laws" are concerned, their position moves from one lattice point to
another.
There is, of course, a danger in introducing differences
between the actual simulation and graphical views of it.
2.3 Time
Time advances in discrete steps. A time, t
 0, is an
integer. At each time step, energy (§2.5) is put into the world and each agent
(§3) is sent an "update yourself" message. 0, is an
integer. At each time step, energy (§2.5) is put into the world and each agent
(§3) is sent an "update yourself" message.
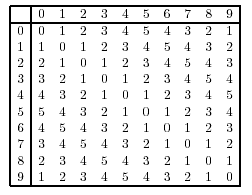
Figure 3: Distance
chart for a one-dimensional space containing 10 points
2.4 Matter
Matter is composed of indivisible units, called atoms.
The units could be considered as
fundamental particles, atoms, or some such. It is more helpful to use a very
loose biological analogy and to think of them as amino acids. However, we retain
the more neutral term "atom" for the formal description.
There are about 26 distinct kinds of
atom and they are denoted by lower case letters: "a", "b" ,
. . . , "z", and a few additional symbols.
Matter is conserved: the total number of atoms
in the world is constant. However, transmutation is possible (§2.5).
Atoms combine to form strings, which are
ordered sequences of atoms. Here are some examples of strings: "ahdj", "zzykkzi",
"g".
Strings might be considered as collections of atoms, or
molecules. But if we pursue the analogy between atoms and amino acids, then
strings are analogous to proteins. We use the neutral term "string" for the
formal description.
If
s is a string, then
|s| is its length, defined to be the number of atoms that
it contains. There are no empty strings: for all strings s, we require |s|
 1. 1.
Atoms might have different
bonding strengths: for
instance "aa" could be a weak bond and "az"
a strong bond. Let's not bother with this complexity unless
it turns out to be useful or necessary.
A
bag is a
collection of isolated atoms (that is, atoms that are not part of strings). The
only important property of a bag is the number of atoms of each kind that it
contains. Thus a bag can be represented by a vector of 26 integers, (na,
nb, . . . , nz)
with 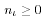 for for
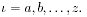 There is a bag
at each lattice point. (There may be other things at lattice points.) There is a bag
at each lattice point. (There may be other things at lattice points.)
A bag could be a collection of strings or string fragments.
The bags are sources of energy, food, etc.
Notation:
We use typewriter font for
literal atoms and italic font for symbols denoting atoms. For example, x
c y stands for the set of strings { xay, xby, . . . , xzy
}.
2.5 Energy
Each atom
a has an
intrinsic energy
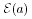 associated
with it. The unit of energy is one erg. The intrinsic energy
corresponds to the position of the letter in the alphabet: associated
with it. The unit of energy is one erg. The intrinsic energy
corresponds to the position of the letter in the alphabet:
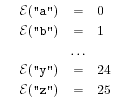
The intrinsic energy is not accessible as such but is
released or absorbed when an atom undergoes transmutation. If an atom c
is transmuted to d, the energy change is

If
 energy is released; if
energy is released; if
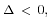 energy is
absorbed. For example, the transmutation "z" energy is
absorbed. For example, the transmutation "z"
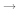 "a" releases 25
ergs and the transmutation "a" "a" releases 25
ergs and the transmutation "a"
 "c" absorbs 2
ergs. Only isolated atoms and atoms in bags can undergo transmutation; atoms in
strings cannot be transmuted. "c" absorbs 2
ergs. Only isolated atoms and atoms in bags can undergo transmutation; atoms in
strings cannot be transmuted.
Energy is
put into the world in a systematic way. Here is a possible algorithm:
. At each time unit, supply E =
A(1 + sin
wt)
ergs to the bag at each lattice point. A and ! are universal
constants.
.
Supply the energy to
the bag by performing each of the following mutations in turn until there are no
more atoms of the required kind or E ergs have been supplied:

Energy is supplied in a systematic rather than random way so
that the agents can evolve to exploit it. With the sinusoidal variation
described above, agents might learn to discriminate "night" and "day". The atoms
mentioned above ("a", "f", "m", "r", "w")
will be quite common and those with high energy ( "r" and "w")
will be useful as energy source for agents. Other atoms, such as "d" and
"q", will be rare; they can be used by agents for signalling and other
purposes.
Atoms react; each reaction either consumes or generates
energy. To obtain energy, a cell absorbs atoms from the its environment, causes
them to undergo reactions that release energy, and returns the products to the
environment. These considerations force a viable agent to:
. obtain energy from appropriate reactions;
. obtain suitable atoms for the reaction;
. dispose of atoms produced.
Let,

For mammals in typical environments, 

Figure 4: Interpreting atoms as quantities. Scalar values may
be multiplied by 25 to obtain integers in [0, 25] according to context.
Note the intentional omission of the zero vector (0, 0, 0).
The effciency of an agent can be modelled as
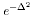 (or perhaps (or perhaps
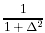 , which is
faster to compute and has a slightly flatter peak) where , which is
faster to compute and has a slightly flatter peak) where
 for some
suitable constant k. Effciency motivates an agent to keep its temperature
close to for some
suitable constant k. Effciency motivates an agent to keep its temperature
close to To;
this in turn requires that the agent can both measure its temperature and modify
it.
During each time interval, the agent's temperature changes
according to 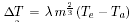 where
where  is
a universal constant and m is the mass of the agent. The exponent is
a universal constant and m is the mass of the agent. The exponent
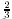 is based on
the idea that the agent with linear dimension s has mass is based on
the idea that the agent with linear dimension s has mass
 and loses and loses
 energy
through its surface.The effect is that the temperature of the agent moves
towards the temperature of the environment. energy
through its surface.The effect is that the temperature of the agent moves
towards the temperature of the environment.
2.6 Quantities
In principle, everything could be encoded by atoms. Since
such an encoding would require large amounts of computation, we avoid it by
defining two kinds of measurement.
Scalars are real numbers and vectors
are triples of real numbers. An atom can be interpreted as either a scalar or a
vector with the values shown in Figure 4.
The components of the vector
v with respect to the coordinate system of the environment are (ux,
uy,
uz).
For a vector v:
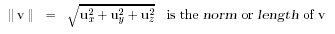
and, if u and
v are vectors, then:
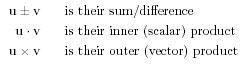
2.7 Diffusion
Perhaps atoms should diffuse between lattice
points. An advantage of diffusion is that it would allow us to simulate
pheromones: pheromones emitted by an agent would diffuse through space, possibly
attracting or repelling other agents. Diffusion would thereby permit a form of
communication akin to smell. A disadvantage is that computing diffusion for all
kinds of atoms would impose a significant computational overhead.
There are at least three possible implementations of
diffusion:
1. Diffusion is random, as in a physical medium that is not
stirred.
2. Diffusion could be directional, as if there was a wind
blowing.
3. Diffusion could be directional, but with a direction
depending on the kind of atom. For example, at each cycle, a proportion p <
1 of atoms of type c could move in the direction given by the
corresponding vector in Figure 4.
Diffusion will probably be ignored in early versions of the
simulation because of its computational overhead.
Page 1, Page 2, Page 3,
Page 4, Page 5
|