Concordia University's DEC LAB: Research at the DEC LAB

The artificial agents are presented; An agent is a collection of cells, each with a defined behavior. These cells are laid out (connected) in a matrix of Grid Cells, and provided with an amount of food initially, a cell using one unit of food per discrete time step. Also in this environment are laid out patches of food; To survive longer, an agent must detect this food, move over top of it, absorb it, and distribute it to the remainder of cells in its body. All cells are capable of local interactions only - a cell communicates or passes food only in its local neighbourhood.

The task presented was chosen for several reasons: (1) It is a highly complicated task, one for which a human designer would experience difficulty; (2) It is a task which easily lends itself to varying phenotypic complexities; (3) Its solution may potentially involve mechanisms found in nature; (4) It combines the need for an internal agent logic embedded as a physical component in the agent.

Additionally, a second model of development is presented, one in which the relation between genotype and phenotype is bijective. The purpose of this inclusion is to evaluate the claims made regarding the developmental process in agent design - to attempt to demonstrate that a developmental model may outperform a bijective model. This is not a claim that the Bluenome method is the best available, however, rather that it is simply a viable option for high-dimensional design problems.

A world is an infinite two-dimensional matrix of Grid Cells. Each world contains one agent at the centre, and a distribution of food. There are no collisions - instead, an agent will pass directly over top of food in the world, possibly absorbing it. Food is parceled in food pieces, each occupying one Grid Cell, having a value of 2*(numTel+1)²food units. Food is distributed differently, depending on world type. Distances between the agent's starting point and the food batches varies between low and high phenotypic complexity runs, the former being placed closer.

Type 0 worlds contain eight batches of food, laid out in a circle surrounding the agent. Type 1 worlds consist of a line of four patches of food, these patches being placed in successively longer distances in one direction. Type 2 worlds consist of four patches of food placed in random locations, slightly farther away than the range of vision of the closest possible eye cell. Type 3 worlds consist of 40 small batches of food distributed randomly in a donut shape surrounding the agent.

An agent is a collection of one or more cells, assumed to be connected. Each cell occupies one grid location. Agents behave as the sum of the behaviours of their cells. So long as one cell is declared "active", an agent is declared "active" - otherwise "inactive".

Cells may be viewed as independent agents of their own right - each maintains a food supply, and executes a particular program based on input and internal variables. Cells may communicate and pass food between adjacent cells (four or eight-neighbourhoods). A cell is "active" (coloured ) if its food supply is greater than zero, otherwise "inactive" (black). An inactive cell will continue to occupy physical space, but will no longer be capable of processing input or output or absorbing food. All cells belong to one of the following classes: Eyes (Green), Nerves (Orange), Feet (Blue), Transports (Red) and Structure Cells (Gray).

Eyes: Eye cells can sense their external environment, and return a boolean value on the basis of the existence of food. However, the presence of other cells within its field of vision will block its ability to sense - hence, an eye cell must be located on the periphery of a agent in order to be capable of functioning.

Nerves: Nerves are cells which accept information from neighbouring eye or nerve cells, and output the (possibly transformed) sum to neighbouring nerve or foot cells. Nerves may have up to four inputs, four outputs, or any combination thereof, determined by connections to eye cells. Nerves output the sum (identity nerves), the negative of the sum (inverse nerves), or the sum plus a random value from {-1, 0, 1} (random nerves).

Feet: Foot cells accept input from all neighbouring nerve cells. Following all other computation, an agent sums the motion of each foot, and moves accordingly (weighted by total size of agent). Forward foot cells move forward (backward for negative input), and rotation foot cells rotate counter-clockwise (clockwise).

Transports: Transport cells manage the collection and distribution of food. At each time step, a transport cell will: collect food from its environment, and pass food to all neighbours in the eight-neighbourhood.

An agent is initialized in the centre of a world, each cell containing 200 units of food, with time defined as zero[1] . The agent next executes the following process at every time step, considering only active cells:

4. Compute the depth of each nerve cell, where a nerve has depth 1 if it is connected to an eye cell, 2 if it is connected to a nerve connected to an eye, etc. Random nerve cells which are not connected to an eye cell are also labeled depth one.

6. All nerve cells of depth one collect input and compute output, continue for each successive depth

Fig. 4.3.1 is an illustration of perhaps the simplest agents capable of finding and absorbing food. As a curiosity, consider Fig. 4.3.2, an agent in a similar situation; This agent's actions would cancel each other out, leading to immobility.[2]

Two methods of development are used: the Bluenome method, as introduced in section 2, and a Bijective method. The bijective method of agent development is a simple model, in which there exists a one-to-one correspondence between elements in the genome, and cells present in the agent. The genome for an agent consists of an

array of integer values, all between 0 and 9, inclusively. A bijective agent is developed by laying out the values of those integers one by one, in a spiral pattern, eventually forming a diamond of area 2*(numTel+1)² - hence, an agent with numTel = 6 will have at most a genotypic and phenotypic complexity of 98; With numTel = 20, a complexity of 882. The genome values are mapped to cell types, where the 0 value is mapped to the empty cell. The spiral layout begins with the central point, and proceeds biased downwards and clock-wise.

4.5 Experimental Setup

The base fitness of an agent in the world is a measure of its size and length of life, relative to a world w.

fitness_base(a)^W = Σ_t numCells(a,t)

(1)

where numCells(a,t) is the number of living cells in agent a at time t. Note: since the amount of food in a world is finite, so is fitness_base.

To help the Bluenome model overcome the development of trivial agents, we introduce a bonus to fitness (for both Bluenome and bijective versions). We define numClasses Î [4] to be the number of those classes for which at least one cell exists in the fully developed agent.

fitness_bonus(a) = numClasses (a)²*20*(numTel+1) ²

(2)

Finally, our fitness function is:

fitness(a)^W = fitness_base(a)^W + fitness_bonus (a)

(3)

In any particular generation, an agent a will be subjected to two worlds, w₁ and w₂., chosen at random (our fitness is stochastic):

fitness(a) = fitness(a) ^W1 + fitness(a) ^W2

(4)

Table 4.5.1 shows the minimum-bonus fitness (the fitness of an agent which has maximized its size and fitness_bonus, but which does not collect any food) and the maximum fitness of agents relative to the parameter numTel.

Evaluation of the Bluenome system involves a series of experiments, differentiated by the model for growth (Bluenome versus Bijective, or bn versus bj), and also by value of numTel. The experiments consisted of one run of each the Bluenome and Bijective systems for numTel ò in {6, 8, 10, 12} (low phenotypic complexity). Additionally, there were three runs for each of the Bluenome and Bijective systems with numTel = 20; (high phenotypic complexity).

Data for the low phenotypic complexity runs (numTel ò in {6, 8, 10, 12}) showed little variance between values of numTel; Hence, only data for the numTel = 6 runs are shown.

As mentioned previously, a problem with the Bluenome model is the failure of many genomes to develop anything non-trivial; Indeed, single cell or single colour organisms appear to be the norm. However, with the addition of the fitness bonus introduced in Section 4.5, selection quickly removes this difficulty. Figure 5.1 shows the population of the first few generations, partitioned into classes on the bases of the number of colours present in the phenotype.

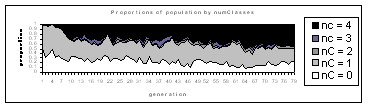
Fig. 5.1 The population of a Bluenome numTel=20 run, partitioned by number of colours (nC) which appear in the phenotype.

In the low phenotypic complexity runs, the bijective runs outperform substantially, as illustrated in Fig. 5.2. Also, Figure 5.3 shows a comparison between maximum time for the numTel = 6 runs - the bijective version typically outperforms the Bluenome version. Contrary to initial expectations, this is not a boon, but instead a drawback. The primary failing of the bijective method is its inability to generate an adequate transport system for distributing food throughout its body. The successes of the bijective model typically involve small groups of cells hoarding food, while no new food is found following time step 200.

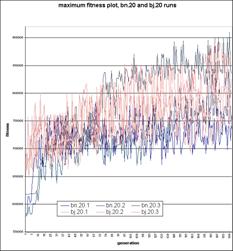
Fig. 5.4 show the fitness plots of the numTel = 20 runs. In these runs, a different trend is seen; Here, the bijective runs all follow a similar course. They begin with some visible evolution, until they reach maximum fitness values in a range of about 720 000 to 850 000 (in all cases prior to generation 100), where they appear to oscillate between values randomly; It appears that the complexity of the space involved exceeds the GAs ability to improve. The lowest of the Bluenome runs shows a similar course to the bijective runs, with some initial evolution and a seemingly random cycling of values following. However, the other two Bluenome plots show a continuous evolution proceeding up to generation 200, potentially continuing beyond this point. Additionally, the highest run quickly shows consistent maximum fitness values which exceed the maximum found in any of the bijective runs. Figure 5.5 clearly shows the continuation of the fitness / time trend - the Bluenome models clearly distribute food between body components more evenly.

An interesting and important property determined from Phase One was that of the Bluenome Model's resistance to changes in environment with respect to agent growth. In Phase Two, an experiment was undertaken which tested a similar situation - that of the re-use of an agent's genome in a differing setting. A population of genomes were selected from a high-phenotypic complexity run (numTel = 20) at a period late in evolution (generation 180). These genomes were re-developed, this time using a value of numTel = 8, rather than 20. The developed agents were evaluated as normal in the numTel = 8 context (that is, using the lower distances for food locations in the worlds). The values obtained are comparable to the numTel = 8 run. In Table 5.1, maximum and mean fitness values are compared between the re-grown agents and a late population from the numTel = 8 run. While the original population outperforms the re-grown agents slightly, the mean and maximum fitnesses of the re-grown agents are comparable to those found in the later stages. Fig. 5.6 shows the first agent of the numTel = 20 run grown with numTel = 8, 20; Visual similarities between the two are immediately visible, and both agents are members of the "Position-then-Rotate Strategy" family of agents (see below).

It has been noted that Phase Two presents an artificial problem for which human designers would experience difficulty; Three (of many) identified agent strategies are presented in the following figures: Fig. 5.7 illustrates a member of the blind-back-and-forth strategy: This strategy may be viewed as a local optimum which often dominates early generations. These agents typically do not include eye or rotation foot cells, relying instead solely on random nerves and forward cells, moving back and forth on the x-axis. This strategy works marginally well for worlds of type 0 and 3, but rarely for other worlds; Fig. 5.8 illustrates a member of the rotate-then-forward strategy, perhaps the most successful strategy found - The agent rotates randomly, until it sees food, then moves forward; Fig. 5.9 illustrates a member of the position-then-rotate strategy, another local optimum: initially the agent moves forward, until it is at the same distance as the first batch of food. Then, it begins to trace a constant circular path - this strategy works poorly on most worlds, except on type zero, where it may be a global optimum.

		Fig. 5.7 Example of the Blind Back-and-Forth Strategy. The dark blue cells are Forward Foot cells, the mid-orange cells Random Nerve cells. The agent contains no Eye of Rotating Foot cells whatsoever, save a single Eye cell near the centre (its location guarantees it will never fire). The single Eye cell is included probably for the sole reason of maximizing fitness _bonus
	Fig. 5.8 An example of the Rotate-then-Forward Strategy. There are two Eye cells on the periphery of the agent - centre left and upper right. These cells are somewhat buried, guaranteeing a narrow focus, and are connected through a large series of Identity Nerve cells to Forward Foot cells. In the centre of the agent are many Random Nerve cells, connected to Rotation Foot cells, providing the random rotation.
Fig. 5.9 Example of the Position-then-Rotate strategy. The agent has Eye cells connected to Forward Foot cells on both the left and right hand side, with more Forward foot cells on the left. Towards the centre of the agent, a series of Random Nerves connect to Rotation Foot cells.