The Computational Aerodynamics Lab

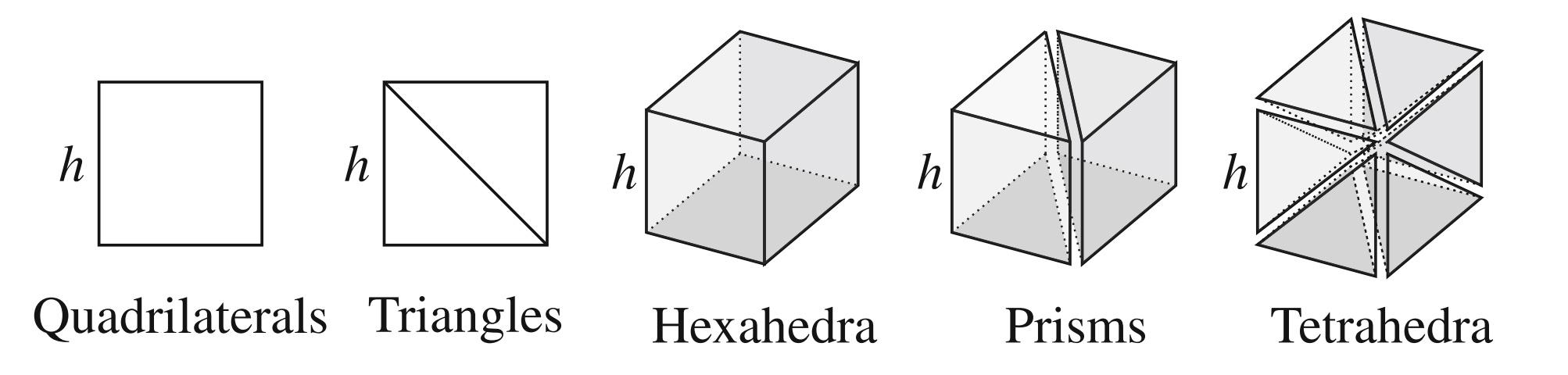
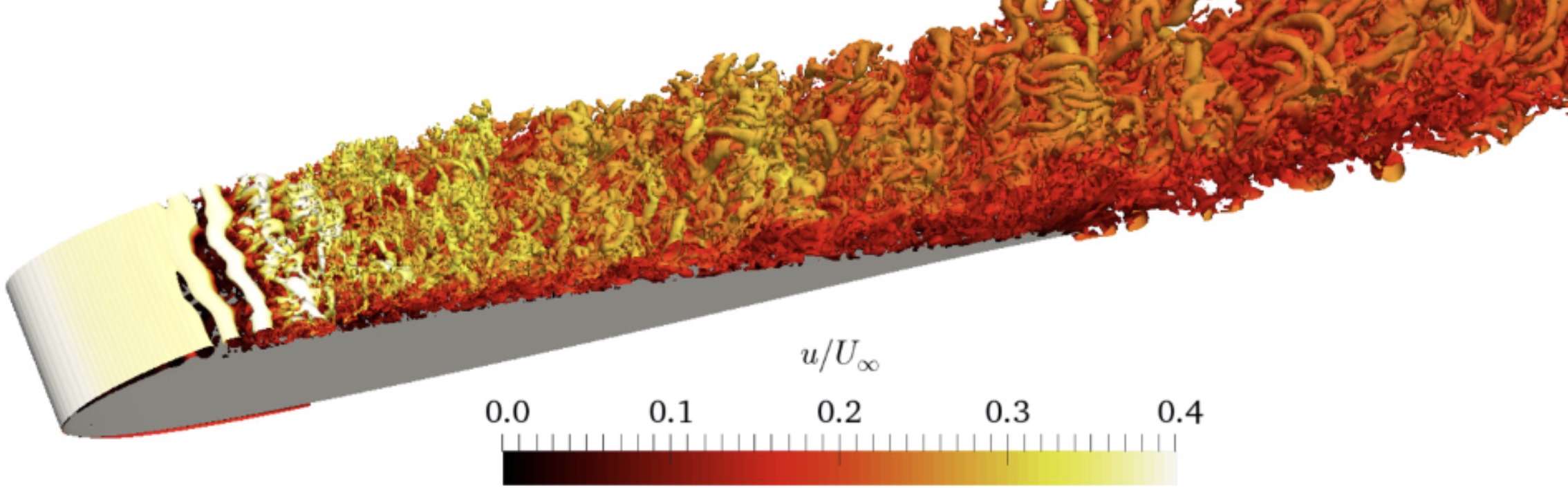
The design of next-generation aircraft relies increasingly on our ability to accurately simulate unsteady turbulent flows. Current industry-standard tools rely on conventional low-order order methods, which have relatively high error. In our lab we work on the development of new high-order methods that have low error per degree of freedom. This means that the solvers we are creating can be orders of magnitude more acccurate and, at the same time, orders of magnitude more accurate that what is currently used in industry.

In addition to accurate solvers, next-generation computational tools require accurate, efficient, and stable schemes for advancing unsteady problems in time. In our lab we develop a range of optimal explicit Runge-Kutta methods and two new families of schemes, Paired Explicit Runge-Kutta (P-ERK) and Accelerated Implicit-Explicit (AIMEX) methods. These schemes are over five times faster than classical methods, and allow us to simulate unsteady flows in a fraction of the computational time previously required.

In addition to performing simulations, next-generation aircraft will require efficient optimization methods. These require determining the effect that changes to design parameters, such as an aircraft shape and configuration, have on its performance. Referred to as sensitivity analysis, we have developed a completely new framework for performing sensitivity analysis of chaotic turbulent flows leveraging reduced order modelling, machine learning, and system dynamics optimization techniques. Our approach has been shown to be thousands of times more efficient than current methodologies, and requires only a fraction of the compute resources.

We develop both gradient-based and gradient-free methods for aerodynamic shape optimization. These allow us to systematically improve the efficiency of airfoils, wings, turbine blades, and other aerodynamic systems used in modern aircraft. Our work is amongst the first to show that optimization can be performed using high-fidelity simulations unsteady chaotic turbulent flows. These results have shown significant improvements in efficiency, such as >30% improvement in the aerodynamic efficiency of wings validated against experimental results.

Turbulent flows contain a wide range of disparate length and time scales. This means that solver resolution requirements change as a simulation evolves, and it is difficult or impossible to know these requirements before running a simulation. Adaptive methods allow the resolution of a simulation to be adjusted by splitting/refining the mesh to better capture local structures. In our work we demonstrate that polynomial adaptation, which allows us to instead change the resolution within an element, is significantly more efficient. Applications to dynamic stall and vertical axis wind turbines shows that this approach is orders of magnitude more efficient that conventional simulations.

Getting accurate results quickly requires leveraging the most power computer hardware architectures that are available. In our lab we focus on Graphical Processing Units (GPUs) and heterogeneous computing with GPUs and clusters of Central Processing Units (CPUs). We have shown that the high-order methods we develop are suitable for petascale simulations on up to 18,000 GPUs and that this approach is orders of magnitude faster than low-order methods on CPUs. All of our solvers are GPU accelerated, enabling us to perform simulations and shape optimization on desktops rather than large-scale supercomputers.