

Next: Entity-Relationship Diagrams Up: No Title Previous: Introduction


Next: Entity-Relationship
Diagrams
Up: No Title
Previous: Introduction
We believe that the semantics of representational devices used for VL theory should be well understood. That is, the meanings of represented language concepts should be unambiguously determined by explicit notational devices whose meanings (semantics) are understood, so that algorithms can operate on the representation in accordance with the semantics of the notation, without needing ad hoc provisions for specific VL domains. In the following we outline a fully formalized theory for describing visual notations that consists of three components. Each component is defined by precise semantics. The definition of objects and relations is based on point-sets and topology. Description logic theory can be based on model-theoretic semantics appealing to first-order logic or using a compositional axiomatization with set theory.
The definition of basic geometric objects (the elementary vocabulary of a visual
notation) usually relies on topology which is itself a basis for defining
relationships between objects. In the following we assume the usual concepts of
point-set topology with open and closed sets [7].
The interior of a set 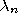 (denoted by
(denoted by 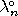 ) is the union of all open
sets in
) is the union of all open
sets in 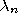 . The closure of
. The closure of
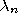 (denoted by
(denoted by
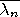 ) is the intersection of all closed sets
in
) is the intersection of all closed sets
in 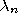 . The complement of
. The complement of
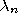 (denoted by
(denoted by
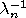 ) with respect to the embedding space
) with respect to the embedding space
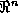 is the set of all points of
is the set of all points of
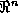 not contained in
not contained in
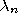 . The
boundary of
. The
boundary of 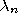 (denoted by
(denoted by
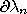 ) is the intersection of the closure of
) is the intersection of the closure of
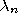 and the closure of the complement of
and the closure of the complement of
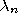 . It follows from these definitions
that
. It follows from these definitions
that
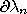 ,
,
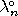 , and
, and
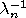 are mutually exclusive and
are mutually exclusive and
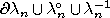 is
is
 .
.
These definitions form the basis for Egenhofer's approach [8] to define topological relations between
objects using the so-called 9-intersection . This method defines
relations between two objects by nine set intersections (every pairwise
combination of interior, boundary, and complement). The following restrictions
apply to every pair of sets. (1)  ,
,
 be n-dimensional and
be n-dimensional and
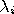 ,
,
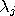
 , (2)
, (2)
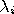 ,
,
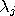
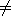 Ø,
(3) all boundaries, interiors, and complements are connected, and (4)
Ø,
(3) all boundaries, interiors, and complements are connected, and (4)
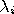 =
=
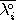 and
and
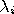 =
=
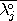 . A major drawback of this approach is
the failure to describe true one-dimensional objects.
. A major drawback of this approach is
the failure to describe true one-dimensional objects.
This was the motivation for the proposal by Clementini et al. [6]. They extended Egenhofer's approach by introducing points and lines as additional object types and the dimension of intersections as new feature for discriminating more cases. Three types of geometric objects are modeled. Regions have to be convex, connected and without holes. Lines and arrows must not be self-intersecting, are either circular or directed, and have exactly two end points. Points are elements of lines and describe their start or end points. The boundary of a point is an empty point-set, the boundary of a line is either an empty point-set (for a circular line) or a point-set consisting of its two end points (for a non-circular line). The boundary of a region is a circular line. The interior of an object is the object without its boundary. In case of points and circular lines their interior is identical to the object itself. Both approaches cannot deal with concave objects.
A third but different approach is based on the work of Clarke about `individuals and points' [9,10]. Clarke's calculus interprets individual variables as ranging over spatio-temporal regions and the two-place primitive predicate, `x is connected with y ', as a rendering of `x and y share a common point '. Randell and Cohn [11] developed their RCC theory based on this single property of connectedness. The RCC theory is a superset of Egenhofer's theory. It can even describe relationships with concave objects by using a convex hull operator.
Of course, there exists a strong interaction between the way of defining basic geometric objects and a set of corresponding spatial relations that can hold between these objects. Each of the above mentioned approaches defines a set of spatial (topological) relationships which are outlined in the next section.
Egenhofer's approach distinguishes eight mutually exclusive relations (out of 92 = 18 different cases). The other cases can be eliminated since the above mentioned restrictions on sets have to hold. The remaining relations cover all possible cases. The 9-intersection is defined as matrix.
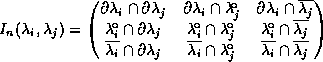
With this definition the eight cases (disjoint, meet, equal covers, contains, overlap) can be easily characterized by the distinction between empty and non-empty intersections. For instance, the contains relation is specified by the 9-intersection as follows.
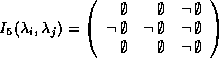
Clementini et al. have to deal with 44 = 256 different cases caused
by taking into account the dimension of intersections. The number can be
reduced to a total of 52 real cases considering the restrictions on objects.
They furthermore reduced this still large number of possible relationships to
five with the help of an object calculus. These five binary topological
relations (touch, overlap, cross, in, disjoint) are mutually exclusive and cover
all possible cases (see [6] for a
proof). For instance, the
in relation is defined as follows: object
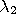 is in object
is in object
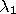 if the intersection between
if the intersection between
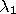 's and
's and
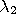 's region is equal to
's region is equal to
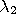 and the interiors of their regions
intersect. It is transitive and applies to every situation.
and the interiors of their regions
intersect. It is transitive and applies to every situation.
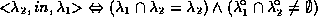
Cohn and Randell define nine spatial relations (that are similar to Egenhofer's set) in terms of a single primitive relation `C(x,y)' read as `x is connected with y'. The authors also introduce an operator `conv(x)' which computes the convex hull of a possibly concave object. Its definition enables reasoning with concave objects. This approach is motivated by the idea that spatial databases might easily compute whether the single relation C(x,y) holds between two objects in the database. Further deductions could be based on this primitive relation. For instance, the relation `x is a part of y' (denoted as P(x,y) ) is defined as follows.
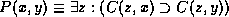
This section gives a brief introduction to some aspects of description logic (DL) theory. We do not attempt to give a thorough overview and formal account of DL theory. However, we try to summarize the notions important for VL theory. We refer to [12,13,14] for more complete information about description logic theory.
DL theories are based on the ideas of structured inheritance networks [15]. A DL can be considered as a term rewriting language restricting the left side of equations to single unique term names. The specification of a DL consists of a set of concepts (or terms), a set of roles (binary relations that may hold between individuals of concepts), a set of disjointness assertions among concepts and among roles, a set of concept membership assertions for individuals, and a terminology, which maps names to specifications of concepts or roles. Concepts may be primitive or defined . A specification of a primitive concept represents conditions that are necessary but not sufficient. The specification of a defined concept represents conditions that are both necessary and sufficient. Primitive and defined roles are similarly specified. If a role holds between individuals, these individuals are referred to as fillers of this role.
Concept specifications may consist of a set of anonymous concept terms or other
concept names. Unary (e.g.  ) and binary
operators (e.g.
) and binary
operators (e.g. 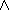 ,
,
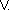 ) are used as connectives. A concept term
can also be given as a restriction of a role.
Number restrictions specify the maximum or minimum number of allowed
fillers (e.g. (
) are used as connectives. A concept term
can also be given as a restriction of a role.
Number restrictions specify the maximum or minimum number of allowed
fillers (e.g. (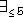 touching) , (
touching) , (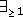 inside)). Value restrictions
constrain the range of roles and allow only fillers that are individuals of a
specific concept (e.g. (
inside)). Value restrictions
constrain the range of roles and allow only fillers that are individuals of a
specific concept (e.g. (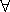 touching
arrow)). Value and number restrictions may also be combined (e.g. (
touching
arrow)). Value and number restrictions may also be combined (e.g. (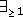 touching arrow) ). The above mentioned
concept specifications are only a subset of all possible specifications.
Figure 1 lists the model-theoretic
semantics of commonly used specification elements (see also Section
3 for the specification of
entity-relationship diagrams). The expressiveness and tractability of a
particular DL depends on the type and allowed combinations of connectives and
restrictions. The underlying algorithms can be NP-complete regarding their
worst-case time complexity with respect to the size of the terms or even
undecidable [14].
touching arrow) ). The above mentioned
concept specifications are only a subset of all possible specifications.
Figure 1 lists the model-theoretic
semantics of commonly used specification elements (see also Section
3 for the specification of
entity-relationship diagrams). The expressiveness and tractability of a
particular DL depends on the type and allowed combinations of connectives and
restrictions. The underlying algorithms can be NP-complete regarding their
worst-case time complexity with respect to the size of the terms or even
undecidable [14].
|
|
Figure 1: Semantics of DL Elements
There exist several theorem provers for special types of DLs. These theorem provers (referred to as DL systems) offer powerful reasoning mechanisms that are based on the DL semantics. DL systems usually distinguish two separate reasoning components. The terminological reasoner or classifier (TBox) classifies concepts with respect to subsumption relationships between these concepts and organizes them into a taxonomy. The TBox language is designed to facilitate the construction of concept expressions describing classes (types) of individuals. The classifier automatically performs consistency checking (e.g. for incoherence, cycles) of concept definitions and offers retrieval facilities about the classification hierarchy. The forward-chaining assertional reasoner or realizer (ABox) recognizes and maintains the type (concept membership) of individuals. The purpose of the ABox language is to state constraints or facts (usually restricted to unary or binary predications) that apply to a particular domain or world. Assertional reasoners support a query language as access to their state. Some query languages offer the expressiveness of the full first-order calculus.
Existing DL systems usually cannot deal with concepts defined with the help of
algebra. For instance, it is not possible to specify a
defined concept SmallCircle that resembles every circle
whose radius is less than 10mm . It is only possible to specify
SmallCircle as primitive concept (which can never
automatically be recognized) and to assert the concept membership externally.
Some DL systems offer extra-logical, user-defined help functions that may
assert the property (radius less than 10mm ) automatically. However,
these functions and their related concepts escape the DL semantics and prevent
any reasoning. For instance, a concept VerySmallCircle resembling
circles with a radius less than 5mm should be recognized as a
specialization (subconcept) of SmallCircle . The idea of incorporating
concrete domains into DL theory is to extend semantics and subsumption in a
corresponding way (see [16]). CTL [17] is an example for a DL system that
combines DL and concrete domains. CTL uses constraint logic programming (CLP)
systems that can cope with systems of (in)equalities over (non)linear
polynomials (e.g. CLP(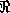 ) [18]). The above mentioned concepts
SmallCircle and VerySmallCircle can be easily specified in
CTL as defined concepts. CTL would immediately recognize the
subsumption relationship between these concepts.
) [18]). The above mentioned concepts
SmallCircle and VerySmallCircle can be easily specified in
CTL as defined concepts. CTL would immediately recognize the
subsumption relationship between these concepts.
We argue that the main characteristics of DL systems are directly applicable to VL theory (see also [3] and Section 3 for a specific application):
Other (but still non-standard) characteristics are also very useful:
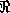 . The need for an extra-logical component
that recognizes geometric features and asserts them to the DL system would
be obsolete.
. The need for an extra-logical component
that recognizes geometric features and asserts them to the DL system would
be obsolete.


Next: Entity-Relationship
Diagrams
Up: No Title
Previous: Introduction