|
4
Results and Analysis
This has two
pats: (a) a comparative empirical study between GA-based feature
selection and GA-based feature weighting algorithms, within the
context of character recognition systems (section 4.1); and (b) an
empirical evaluation of the effectiveness of GA-based feature
selection for off-line optimization of character recognition systems
(section 4.2).
4.1 Comparative Study Results
Following are
four empirical studies that compare the performance of GA-based
feature selection (GFS) to GA-based feature weighting (GFW), with
respect to (a) the number of eliminated features, and (b)
classification accuracy. In all the experiments, 1-NN stands
1-nearest neighbour classifier (i.e. no GA-based optimization), FS
stands for GFS, and XFW stands for GFW with an X-number
of weight levels.
4.1.1 The effect
of varying the number of values that weights can take on the number
of selected features
It is known
that feature selection, generally, reduces the cost of
classification by decreasing the number of features used (Dash &
Liu, 1997). GFW methods should, theoretically, have the same
potential (because GFS is a special case of GFW). However, it has
been argued that in reality, GFS eliminates many more features than
GFW. How many more, though, is unknown. Since the essential
difference between GFS and GFW is the number of values that weights
can take, we decided to study the relationship between the number of
weight values and the number of eliminated features. We also tested
a method for increasing the ability of GFW to eliminate features.
The database used in this experiment is DB1, which contains a
relatively large number of features (64). The error estimation
method used is the leave-one-out cross validation technique. It is
applied to the training data itself. The number of training samples
is 200. It is applied to the training data. The resultant weights
are assessed using a validation data set of size 200. This set is
new, in that it is not used during training. The results of the
experiments are presented in tables 1 and 2. The following
description of columns applies to the contents of both tables. The
first column presents the method of feature selection or weighting.
It is (a) 1-NN, which means that a 1-NN classifier is applied
directly to the full set of features, with no prior selection or
weighting; (b) FS, which means that feature selection is applied
first before any classification is carried out; or (c) FW (with
different weighting schemes), which means that feature weighting is
applied prior to 1-NN classification. The second column, increment
value, shows the difference between any two successive weight
levels. The third column presents the total number of weight levels
that a weight can take. A weight can take on any one of a discrete
number of values in the range [min, max]. The difference between any
two consecutive values is the 'increment value'. The fourth column
is simply the inverse of the number of levels, which is termed:
'probability of zero'; the reason for such terminology will be made
clear presently. The fifth and sixth columns show classification
accuracies for both training and testing phases, respectively. The
final column presents the number of eliminated features, which we
call the number of zero features. This is easily computed by
subtracting the number of selected features from the total number of
features (64). It is worth noting that values shown in columns 5-7
are the average values of five identical runs.
|
Method of Selection/
Weighting
|
Increment Value
|
Number of Levels
|
Probability of Zero
|
Accuracy of Training
|
Accuracy of
Testing
|
Number of Zero Features
|
|
1-NN
|
-
|
-
|
-
|
97.5
|
84.5
|
-
|
|
FS
|
1
|
2
|
1/2
|
99.4
|
84.8
|
27
|
|
FW
|
0.5
(1/2)
|
20+1
|
1/21
|
99
|
84
|
3
|
|
FW
|
0.25
(1/4)
|
40+1
|
1/41
|
98.9
|
83.8
|
1
|
|
FW
|
0.125
(1/8)
|
80+1
|
1/81
|
99
|
83.5
|
0
|
|
FW
|
0.0625
(1/16)
|
160+1
|
1/161
|
98.9
|
83.9
|
0
|
|
FW
|
0.03125
(1/32)
|
320+1
|
1/321
|
98.6
|
83.2
|
0
|
|
FW
|
0.015625
(1/64)
|
640+1
|
1/641
|
99
|
83.2
|
0
|
|
FW
|
0.0078125 (1/128)
|
1280+1
|
1/1281
|
98.9
|
83.7
|
0
|
|
FW
|
0.0039
(1/256)
|
2560+1
|
1/2561
|
98.2
|
83
|
0
|
Table 1:
Accuracy of Recognition and Number of Zero Features for Various
Selection and Weighting Schemes
|
Method of Selection/
Weighting
|
Increment Value
|
Number of Levels
|
Probability of Zero
|
Accuracy of Training
|
Accuracy of
Testing
|
Number of Zero Features
|
|
FS
|
1
|
2
|
1/2
(0.5)
|
99.4
|
84.8
|
27
|
|
FW:
three discrete values: 0, 0.5, and 1.
|
0.5
|
3
|
1/3
(0.33)
|
97.8
|
83.3
|
18
|
|
FW:
values belong to [0, 10], with weights < 1 forced to 0.
|
0.125
|
81
|
8/81
(0.098)
|
98.1
|
84.2
|
7
|
|
FW:
values belong to [0,10].
|
1
|
11
|
1/11
(0.09)
|
98.5
|
82.8
|
5
|
|
FW: six
discrete values: 0, 0.2, 0.4, 0.6, 0.8, and 1.
|
0.2
|
6
|
1/6
(0.166)
|
98.3
|
83.3
|
8
|
|
FW: six
discrete values: 0, 0.2, 0.4, 0.6, 0.8, and 1, with weights <
0.8 forced to 0.
|
0.2
|
6
|
4/6
(0.66)
|
96.6
|
81.6
|
38
|
|
FW: six
discrete values: 0, 1, 2, 3, 4, and 5.
|
1
|
6
|
1/6
|
97.9
|
83.4
|
9
|
|
FW: six
discrete values: 0, 1, 2, 3, 4, and 5, with weights < 4 forced
to 0.
|
1
|
6
|
4/6
(0.66)
|
97.4
|
81.2
|
34
|
Table 2:
Accuracy of Recognition and Number of Zero Features for Various
Selection and Weighting Schemes, Some with Low Weight Forced to Zero
The following
observations can be made, based on the results in table 1.
-
Although
feature selection succeeded in eliminating roughly 42% of the
original set of features (27 out of 64), classification accuracy
did not suffer as a result. On the contrary, training accuracy
increased to 99.4% from the 97.5% realized by the 1-NN alone.
Also, testing accuracy increased to 84.8% from the 84.5% value
achieved by the 1-NN classifier (alone).
-
FS far
outperforms FW in terms of the number of zero features. Also,
training accuracies achieved by both FS and FW were better than
those achieved by the 1-NN classifier (alone). Using the testing
set, the accuracy levels achieved by FW range between slightly
worse to worse than the accuracy levels achieved by the 1-NN
classifier. In contrast, the accuracy levels achieved by FS are
slightly better than those of the 1-NN classifier alone (and hence
better than those of FW as well).
FS does not
eliminate features at the expense of classification accuracy. This
is because the fitness function used is dependent on classification
accuracy only. There is no selective pressure to find weight sets
that are (e.g.) smaller.
The following
observations can be made, based on the results in table 2.
-
The number
of zero features is greater in cases where the number of possible
weight values is countably finite, than where weights take values
from an infinitely dense range of real numbers.
-
Also,
increasing the number of levels beyond a certain threshold (81),
reduces the number of zero features to nil.
-
When we use
FW with discrete values (0,1, 2, 4, 5), and forced all weights
less than four to zero, FW actually outperforms FS in the number
of zero features. It is worth noting that the Probability of Zero
for this FW configuration is 0.66, compared to 0.5 for FS.
-
Regardless
of the method of selection or weighting, the number of zero
features appears to be influenced by only the number of levels
that weights can take. For example, using six discrete values, but
in two different configurations, (0, 0.2, 0.4, 0.6, 0.8, and 1)
and (0,1,2,3,4,5, and 6), produces almost identical numbers of
zero features: 8 and 9, respectively.
All the points
above suggest that, generally, the greater the total number of
weight levels, the less likely it will be that any of the features
will have zero weights. Whether this apparent relationship is
strictly proportional or not is investigated further below.
Using data
from tables 1 and 2 the relationships between the number of zero
features and the number of levels has been drawn. This relationship
is depicted in Fig. 1a.
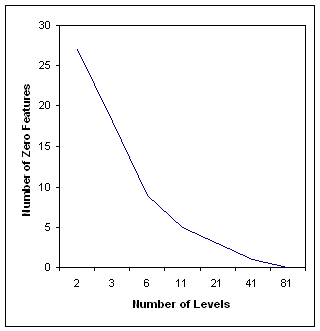

Figure 1a:
Relationship
between Number of Weight Levels and Actual Number of Zero Features
It represents
the empirical relationship between the number of weight levels and
the actual number of zero (or eliminated) features. The relationship
is close to an inversely proportional one. This represents credible
evidence that (a) the number of eliminated features is a function
of, mainly, the number of weight levels; and hence (b) that the main
reason behind the superiority of feature selection over feature
weighting (in eliminating features) is the smaller number of weight
levels FS uses.

Figure 1b:
The Number of
Eliminated (or Zero) Features as a Function of the Probability of
Zero
It further
appears, from Figure 1b that the relationship between the 'probability' of zero features and the actual number of
zero features is roughly linear, though not strictly proportional.
If it were strictly proportional then the 'probability' of zero
would likely represent a real probability, hence the term. As things
stand, the empirical results support the claim that the underlying
probability distribution of weight values is (roughly speaking)
uniformly random.
In conclusion,
it is possible to state that feature selection is clearly superior
to feature weighting in terms of feature reduction. The main reason
for this superiority appears to be the smaller number of weight
levels that feature selection uses (2), compared to feature
weighting (potentially infinite). However, it is possible to make
feature weighting as effective as feature selection in eliminating
features via, for example, the forcing of all weights less than a
given threshold to nil.
4.1.2 Studying
the performance of both FS and FW in the presence of irrelevant
features
For most classification problems, relevant features are not known in
advance. Therefore, many more features than necessary could be added
to the initial set of candidate features. Many of these features can
turn out to be either irrelevant or redundant. (Kohavi & John, 1996)
define two types of relevant (and hence irrelevant) features. They
state that features are either strongly relevant or weakly
relevant, otherwise they are irrelevant. A strongly relevant
feature is one that cannot be removed without degrading the
prediction accuracy of the classifier (in every case). A weakly
relevant feature is a feature that sometimes enhances
accuracy, while an irrelevant feature is neither strongly nor weekly
relevant. Irrelevant features lower the classification accuracy
while increasing the dimensionality of the problem. Like
irrelevant features,
redundant
features have the same drawbacks of accuracy reduction
and dimensionality growth. As a result, removing these features by
either feature selection or weighting is required. (Wettschereck et
al., 1997) claim that domains that contain either a) sub-sets of
equally relevant (i.e. redundant) features or b) any number of
[strongly] irrelevant features are most suited to feature selection. We intend to investigate this claim by comparing the
performance of GFS to that of GFW in the presence of irrelevant and
(later) redundant features. It is
important to indicate that Wilson and Martinez (1996) compares the
performance of genetic feature weighting GFW with the non-weighted
1-NN for domains with irrelevant and redundant features. They use GA
to find the best possible set of weights, which gives the highest
possible classification rate. In the presence of irrelevant and
redundant features, they show that GFW provides significantly higher
results than the non-weighted algorithm. However, they do not
compare GFW to GFS for classification tasks with irrelevant or
redundant features. Therefore, we are presented with a good chance
to see how far feature selection tolerates irrelevant and redundant
features, as opposed to feature weighting.
In this experiment we use the dataset that contains 6 features
within DB3. We gradually add irrelevant features, which are assigned
uniformly distributed random values. We observe the
classification accuracy for GA-based feature selection, GA-based
feature weighting, as well as a 1-NN classifier (unaided by any kind
of FS or FW). During GA evaluation, we use the holdout method of
error estimation. The samples are split into three sets, a training
set, a testing set, and a validation set. The training samples are
used to build the nearest neighbour classifier, while the testing
samples are used during GA optimization. After GA optimization
finishes, a separate validation set is used to assess the weights
(coming from GA optimization). The number of training samples is
1000, the number of testing samples is 500, and the number of
validation samples is 500. To avoid any bias due to random
partitioning of the holdout set, random sub-sampling is performed.
The random sub-sampling process is repeated 5 times, and the
accuracy results reported represent average values of 5 runs.
The results of
experimentation are shown in figures 2 and 3 below. Figure 2
represents classification accuracy (of the various selection and
weighting schemes) as a function of the number of irrelevant
features included in the initial set of features. Figure 3
represents the number of eliminated features as a function of
irrelevant features. In the figures, FW3 stands for feature
weighting using 3 discrete equidistant weight levels (0,0.5, 1), FW5
stands for FW with 5 discrete equidistant weight levels, while FW33
stands for FW with 33 discrete equidistant weight levels.
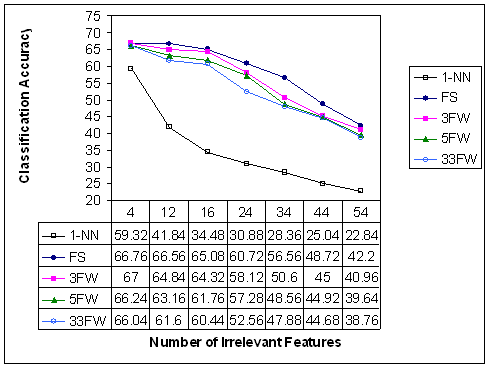
Figure 2:
Classification Accuracy as a Function
of the Number of Irrelevant Features

Figure 3:
Number of Eliminated Features as a
Function of the Number of Irrelevant Features
From figures 2
and 3 we can conclude the following:
-
As the
number of irrelevant features increases, the classification
accuracy of the 1-NN classifier rapidly degrades, while the
accuracies attained by FS and FW slowly degrade. Therefore,
nearest neighbour algorithms need feature selection/weighting in
order to eliminate/de-emphasize irrelevant features, and hence
improve accuracy.
-
As the
number of irrelevant features increases, FS outperforms
every feature weighting configuration (3FW, 5FW and 33FW), with
respect to both classification accuracy and elimination of
features. However, when the number of irrelevant features is only
4, 3FW returns slightly better accuracies than FS. This changes as
soon as the number of irrelevant features picks up.
-
When the
number of irrelevant features is 34, the difference in accuracy
between FS and the best performing FW (3FW) is considerable
at 6%.
-
As the
number of weight levels increases, the classification accuracy of
FW, in the presence of irrelevant features, decreases.
-
As the
number of weight levels increase, the number of eliminated
features decreases.
-
When the
number of irrelevant features reaches 54, the classification
accuracy of FS drops to a value comparable to that of other
FW configurations. However, the number of eliminated features by
FS continues to outperform any other FW configuration.
-
The gap in
the number of features eliminated by FS compared to FW and 1-NN increases as the number of irrelevant features increases.
Why does feature
weighting perform worse than feature selection in the presence of
irrelevant features? Because it is hard to explore a space of real
valued weights in  when d is large. R is the number of
real-valued weights, and d is the number of features.
Whereas, in the case of feature selection, the search space is when d is large. R is the number of
real-valued weights, and d is the number of features.
Whereas, in the case of feature selection, the search space is
 in size. For example, with 10 irrelevant
features, the search space for FS is in size. For example, with 10 irrelevant
features, the search space for FS is
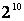 (=1024) compared to (=1024) compared to
 (=25937424601) for FW using 11 weight levels.
Moreover, a single increase in the number of weight levels from 2 to
3 increases the size of the search space form (=25937424601) for FW using 11 weight levels.
Moreover, a single increase in the number of weight levels from 2 to
3 increases the size of the search space form
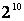 (=1024) to (=1024) to
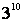 (=59049). As witnessed earlier, as the number of
weight levels increases, the number of eliminated features
decreases. Therefore, FS will always eliminate more features than
FW, given the same computational resources. In addition, in
applications with large sets of features (which implies a high
degree of irrelevancy/redundancy among features),
it has been shown that feature selection had better results than
IB4, an on-line feature weighting algorithms (Aha & Banket, 1994). (=59049). As witnessed earlier, as the number of
weight levels increases, the number of eliminated features
decreases. Therefore, FS will always eliminate more features than
FW, given the same computational resources. In addition, in
applications with large sets of features (which implies a high
degree of irrelevancy/redundancy among features),
it has been shown that feature selection had better results than
IB4, an on-line feature weighting algorithms (Aha & Banket, 1994).
We conclude
that in the presence of irrelevant features, feature selection and not feature weighting is the technique most suited to
feature reduction.
Furthermore, it is necessary to use some method of feature
selection before a 1-NN or similar nearest-neighbour classifier is
applied, because the performance of such classifiers degrades rapidly in the presence of irrelevant features. Since it has
been shown that GA-based feature selection is effective in
eliminating irrelevant features (here and in the literature), it
seems sensible to try a GA (at least) as a method of feature
selection before classification is carried out using nearest-neighbour
classifiers.
Page 1, Page 2,
Page 3,
Page 4
|

![]()
