4.1.3
Performance of both FS and FW in the presence of redundant features.
In this
experiment we used the dataset with 6 features in DB3. We randomly
selected one feature from the dataset, and repeatedly added this
features several times. We observed the accuracy of classification
for GA-based FS, GA-based FW, as well as the unaided 1-NN
classifier. The error estimation method is the same as that used in
section 4.1.2 (above). The results of experimentation are shown in
figures 4 and 5. Figure 4 shows the empirical relationship between
the number of redundant features, present in the initial set of
features, and the classification accuracy of the 1-NN classifier,
acting alone, and with the help of GA-based feature
selection/weighting. Figure 5 presents the relationship between the
number of redundant features, and the number of features eliminated
by FS and FW. A 1-NN, on its own does not eliminates any features,
of course.
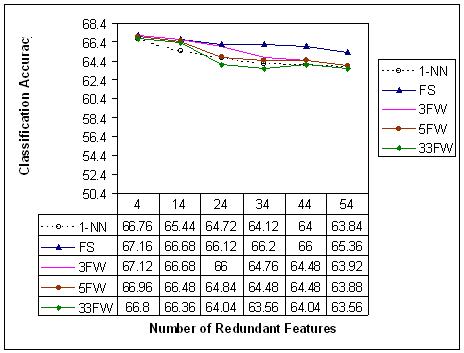
Figure 4:
Classification Accuracy as a Function
of the Number of Redundant Features
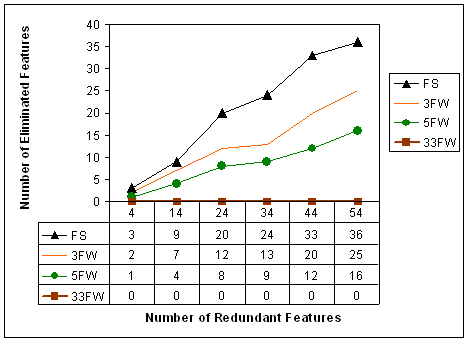
Figure 5:
Number of Eliminated Features as a
Function of the Number of Redundant Features
From figures 4
and 5, the following observations can be drawn:
·
Contrary to the case of irrelevant features, the classification
accuracy of the 1-NN classifier degrades very gradually,
as a function of the number of redundant features.
·
In
experiments with 4, 14 and 24 redundant features, FS classification
accuracies are almost identical to those achieved by 3FW.
However, for the same number of redundant features, the other
feature weighting configurations returned classification accuracies
that are worse, but only slightly.
·
FS
outperforms all other FW configurations in experiments where
the number of redundant features is 34 or greater.
·
As
the number of weight levels increases, the classification
accuracy of the feature weighting configurations slightly decreases.
·
Although the difference in classification accuracy between FS and FW
is not very large, the difference in terms of the number of
eliminated features (shown in fig. 5) is significant.
·
The
difference in performance between FS and FW increases
as the number of redundant features climbs. Finally, when the
number of redundant features reaches 54, FS succeeds in eliminating
34 redundant features, 11 more than the best performing FW
configuration (3FW).
Why does not the
performance of the 1-NN classifier quickly degrade as the number of
redundant features increases? The reason is that adding copies of an
existing feature repeatedly to a set of features (to act as
redundant features) is like giving that feature an added weight
equal to the number of copies. For example, if a certain feature is
added 20 times, this has the same effect as using this feature once,
but multiplied by a weight of 20. On the other hand, completely
irrelevant features add randomness and noise to the feature set,
which cause higher classification error rates. Though the presence
of redundant features in the training data might not significantly
decrease the accuracy of the classification algorithm, it will
certainly worsen the problem of dimensionality. Moreover, giving a
certain feature higher weight simply because it was repeated is
considered to be a random procedure (Wilson
& Martinez, 1996).
In conclusion,
the classification accuracy of a 1-NN classifier does not suffer
greatly as a result of having a significant number of redundant
features in the (original) feature set. However, due to the other
problems associated with redundant features increased dimensionality
(and hence computational cost), and arbitrariness of procedure, as
well as slightly worse classification accuracies, it is recommended
that a GA-based feature selection method be used to eliminate as
many of the redundant features as possible. It is clear that the
best suited feature selection/weighting methods for such a task are
FS and 3FW. Which one is chosen depends on the need for real-valued
weights vs. computational efficiency.
4.1.4
Performance of both FS and FW for Real-World and Regular Databases.
(Wettschereck et al., 1997) state that feature
weighting (GA-based or not) is more suitable than feature selection
for domains where features have a wide range of relevance. On the
other hand, (Kohavi,
Langley & Yun, 1997) show
that increasing the number of weights above two rarely reduces
classification error, for many real world datasets. They show that
using only two weights (which is equivalent to feature selection)
gives better results than increasing the set of weights. It is worth
noting that the results of (Kohavi et al., 1997) are for small
datasets (with less than 300 training samples), and use a best-first
search algorithm. In contrast, we intend to compare feature
selection to feature weighting using real-world and regular
databases, with 1000+ training samples, and using GAs as a search
method.
Presented here
is a study of the classification accuracies achieved by the 1-NN
classifier and the various GA-based feature selection (FS) and
weighting (FW) configurations. The focus in this study is on
assessing the true real-world performance of such configurations.
This requires (a) that real-world databases (containing
human-generated samples) are used, and (b) that any results achieved
using training sets are checked against separate results obtained
with new (unseen) validation sample sets. The resultant accuracies
for training and validation sample sets are displayed in figures 6
and 7. The database used for figures 6 and 7 was the 6 feature
dataset in DB3. For figures 8 and 9, we used DB2. The error
estimation method is the leave-one-out cross validation. It was
applied to 1000 training samples. The best weights are tested using
a separate set of 500 validation samples. To avoid bias, we randomly
selected different training/validation sets for each experimental
run. Each experiment is repeated 5 times, and the results reported
are average values for those. The symbols on the X-axes indicate the
following:
-
1-NN:
1-nearest neighbour classifier (no GA).
-
FS: FS using
2 weights (0,1).
-
FW3: FW
using 3 weights (0,0.5,1).
-
FW5: FW
using 5 weights (0,0.25,0.5,0.75,1).
-
FW17:
FW using 17 weights in [0,1], and an increment value of 0.0625
(1/16).
-
FW33:
FW using 33 weights in [0,1], and an increment value of 0.03125
(1/32).

Figure 6:
Training Classification Accuracies for
the Various Feature Selection and Weighting Methods (using DB3)
Results show that classification
accuracy is worst for the (unaided) 1-NN, but better for FS and FW. The trend
line highlights the fact that the greater the number of weight levels the
higher the training accuracy rate achieved. Finally, it appears that
classification accuracy could not be improved much by increasing the number of
weights beyond 17; the difference in classification accuracy between 17FW and
33FW is 0.02, which is insignificant.

Figure 7:
Validation Classification Accuracies for the Various Feature
Selection and Weighting Methods (using DB3)
Results show that
classification accuracy is best for the (unaided) 1-NN and FS, but
worse for FW. The trend line highlights the fact that the greater
the number of weight levels the lower the validation accuracy rate
achieved. Finally, it appears that classification accuracy cannot be
further degraded by increasing the number of weights beyond 17;
there is no difference in classification accuracy between 17FW and
33FW. These results are the opposite of those found in figure 6!
This means that FW is returning good accuracy results for training
data, but then returning bad results for validation data. Also, it
is the performance of a classifier on validation data that truly
reflects its (real-world) predictive capacity.
To verify
these interesting results, we ran the same set of experiments on
another database (DB2). This is to ensure that the above results are
independent of the particular sample database used. The results are
shown in figures 8 and 9. It emerges that the results of these
experiments indeed confirm the results of figures 6 and 7.

Figure 8:
Training Classification Accuracies for
the Various Feature Selection and Weighting Methods (using DB2)

Figure 9:
Validation Classification Accuracies for the Various Feature
Selection and Weighting Methods (using DB2)
Based on the
results of figures 6-9 we make the following observations.
-
For the
validation sets, the classification accuracy of FS was slightly
better than all the FW settings for both databases. However, it
was the same as 1-NN for DB3 and slightly worse for DB2.
-
For the
training sets all FW settings have better classification accuracy
than FS.
-
Increasing
the number of weight levels led to a slight decrease in the
classification accuracy of the validation sets.
-
Increasing
the number of weights has led to slight increase in the
classification accuracy of the training sets.
We believe the
interesting disparity between training and validation results is due
to over-fitting. FW allows for a finer-grain representation of the
search space, but at the expense of an increased classification
error rate. In other words, what we are faced with here is a typical
bias vs. variance tradeoff (Geman, Bienenstock & Doursat,
1992). Classification error can be decomposed into two components,
bias and variance. Bias measure how much the error
estimation deviates from the true value, whereas the variance
measures how much variability classification shows for different
training samples. For example, assume that we have an infinite
number of classifiers built from different training sets of the same
size. The bias of a learning algorithm is the expected error of the
combined classifiers on new data. The variance, on the other hand,
is the expected error due to the particular training set used.
Therefore using a small number of weights will increase the bias due
to the lack of representation of the space. However, this will also
reduce variance, which in turn reduces the possibility of
over-fitting of data (Kohavi et al., 1997). In contrast, allowing
many weights will reduce bias but will also increase variance, and
the probability of over-fitting.
(Kohavi et
al., 1997) also illustrate that increasing the number of weights
above two hardly ever decreases classification errors. In their
study they show that with 10 weights levels, FW fails to outperform
FS on 11 real-world databases. They conclude that, "On many natural
data sets, restricting the set of weights to only two
alternatives-which is equivalent to feature subset selection-gives
the best results". Though we used different search methods and
larger datasets than those used by Kohavi et al., we get similar
results and conclusions.
In addition,
we should take into account that the databases we are using to
report our results are handwritten character recognition databases.
This means that there are many variants of letter shape, size, and
generally, style. Also, different writers have different writing
styles. For the letters of an alphabet, there are nearly an
unlimited number of variations. Thus, feature weighting over-fits
the training data by finding suitable weights, but these weights
obtained do not generally represent the underlying distribution due
to the large variance among the training samples.
On the other
hand, other papers have shown that feature weighting using GAs yield
a slightly better classification accuracy than feature selection for
real-world databases. For example, (Punch et al., 1993)
perform tests using binary and real-valued weights (with weights in
[0,10]). Their database consisted of images of soil samples. Their
results show that the error rates obtained using real-valued weights
are better than those with binary weights. Also, (Komosinski &
Krawiec, 2000) provide further evidence that feature weighting is
somewhat better than selection when applied to a brain-tumor
diagnoses system. Their results confirm that feature weighting
(using weights in [0,9]) leads to somewhat better classification
accuracy rates than just feature selection.
However, several points must be raised here. First, results reported
in (Komosinski & Krawiec, 2000) are those of GA evaluation. No
validation tests were done to test the resultant weights on separate
data sets. In fact, (Kohavi & Sommerfield, 1995) have noticed this
fact and states that separate holdout sets, which were never used
during the feature selection/weighting, should be used in the final
test of performance. Second, results reported by (Punch et
al., 1993) were performed on validation samples, which were randomly
drawn from the training samples. This also has the same
biased effect on the results. Third, the improvement in
classification accuracies mentioned in both papers for FW over FS is
so little that it does not, in itself, provide final evidence that
FW gives better results than FS on real datasets. Komosinski &
Krawiec reports classification accuracies of 83.43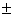 1.93 and 77.83 1.93 and 77.83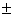 2.03 (for two datasets) for FW, vs.
accuracies of 80 2.03 (for two datasets) for FW, vs.
accuracies of 80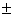 1.22 and 75.7 1.22 and 75.7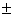 1.64 for FS. While Punch et al. reports a
classification error rate for FW of 0.83% and 2% for training and
testing respectively, those of FS were 1.66 and 3.2% for training
and testing. 1.64 for FS. While Punch et al. reports a
classification error rate for FW of 0.83% and 2% for training and
testing respectively, those of FS were 1.66 and 3.2% for training
and testing.
In conclusion,
despite the fact that feature weighting has the best training
classification accuracies, feature selection is better in
generalization, and hence more suited to real-world applications (in
which most data is new). This is because FW overfits the training
data, losing generalizability in the process. Therefore, it is
advisable to use 2 (FS) or 3 (3FW) weight levels at most, as (Kohavi
et al., 1997) recommend.
4.2 Feature
Selection Evaluation Results
The following
are two empirical studies that study the effectiveness of GA-based
feature selection (GFS) with respect to (a) finding a provably
optimal set of features, and (b) doing so within an acceptable time
frame, for off-line applications (e.g., pre-release optimization of
character recognition software).
4.2.1 Convergence of FS to
an Optimal or Near-Optimal Set of Features
In the context
of feature selection, several comparative studies involving Genetic
Algorithms and other search and optimization algorithms are
available. (Vafaie & De Jong, 1993) show that GA outperforms
sequential backward selection in robustness. They demonstrate that
genetic algorithms improve robustness of feature selection without a
major increase in computational complexity. Moreover, (Handels et
al., 1999) compare a number of feature selection methods: Genetic
Algorithms other heuristic searches, and 'greedy' methods (forward
and backward searches). Their domain of application is diagnosis of
skin tumors. The best classification accuracy is obtained by the GA.
(Estevez & Fernandez, 1999) perform a comparison between Genetic
Algorithms, statistical methods and the leave-one-feature-out
approach, all in the context of classifying wood board defects. The
GA gives the best performance among the three techniques, but at the
expense of high computational complexity. (Kudo & Sklansky, 2000)
provide a recent comparison of different feature selection
algorithms (including GAs) for large feature spaces. The authors
conclude that Genetic Algorithms are more suited than other feature
selection algorithms for problems with more than 50 features.
However, for small (0-19 features) and medium (20-49) cardinality,
GAs though useful, are too slow to justify their use.
It is clear
from the literature that several studies exist comparing GA with
other feature selection search algorithms, so it not our intention
to repeat such work. However, there is a need to determine whether
or not GFS does indeed return optimal or near-optimal feature
sub-sets. This necessitates an exhaustive search of the features
space in order to find one or more bona fide optimum feature
sub-set. These can then be used to assess (with certainty) the
optimality of the best GFS-generated feature sub-sets.
For the experiments in sections 4.2.1 and 4.2.2, we used a single
training/testing set of size 1000 and 500, respectively. The numbers
of features used in the searches are 8, 10, 12, 14, 16, and 18. We
used features from more than one dataset in DB3 for that purpose.
There is no need to have a separate validation set since our
objective here is to evaluate optimal performance, and not test
generalizability.
|
Number of Features
|
Best Exhaustive
(classification rate)
|
Best GA
(classification rate)
|
Average GA (for 5
runs)
|
|
8
|
74
|
74
|
74
|
|
10
|
75.2
|
75.2
|
75.2
|
|
12
|
77.2
|
77.2
|
77.04
|
|
14
|
79
|
79
|
78.56
|
|
16
|
79.2
|
79
|
78.28
|
|
18
|
79.4
|
79.4
|
78.92
|
Table 3:
Best
Classification Accuracy Rates Achieved by GA and Exhaustive Search
The results
presented in table 3 compare the best and average accuracy rates
achieved via GA-based feature selection (FS) with the optimal
accuracy rate found via an exhaustive search of the entire feature
space.
Comparing the numbers in the best GA column with the numbers in the
best exhaustive column exhibits the success of the GA as a feature
set optimizer. In every case but one (when the number of features is
16), the best accuracy achieved by the GA was identical to that
found an exhaustive search of the feature space. Furthermore, the
fact that the worst average GA value is less than 0.8 of a
percentage point away from the optimal value means that the GA was
consistently able to return optimal or near-optimal values of
accuracy. Hence, GA-based feature selection consistently converges
to an optimal or near-optimal set of features.
4.2.2 Convergence of FS to
an Optimal or Near-Optimal Set of Features within
an Acceptable Number of Generations.
In general,
the run time for the GA is proportional to the number of features,
number of generations and size of the population (Kudo & Sklansky,
2000). Moreover, the time complexity of the nearest neighbour
classifier is proportional to ( x d), where t is the number of
training instances and d is the number of features used. So a GA that
is applied in a wrapper configuration to a nearest neighbour
classifier spend most of its time running the nearest neighbour
classifier (Brill, Brown & Martin, 1992). Below, we list those
factors that affect the time complexity of our GFS or GFW: x d), where t is the number of
training instances and d is the number of features used. So a GA that
is applied in a wrapper configuration to a nearest neighbour
classifier spend most of its time running the nearest neighbour
classifier (Brill, Brown & Martin, 1992). Below, we list those
factors that affect the time complexity of our GFS or GFW:
-
Number of
generations
-
Population
size
-
Number of
features
-
Number of
training instances
In this
evaluation, we will investigate the relationship between the number
of features (in the original set) and the number of generations
required to reach an optimal or near-optimal sub-set. We will do
that while keeping the two other factors (i.e. population size and
number of training instances) constant.
The results of
experimentation are shown in table 4. The second column of table 4
shows the best (i.e. optimal) classification accuracy rates attained
using an exhaustive search, whereas the third column displays the
duration of that search. The fourth column contains the best results
achieved via a GA-based search, while the fifth column contains the
time it took the GA to attain those values.
|
Number of Features
|
Best Exhaustive
(optimal and sub-optimal)
|
Exhaustive Run Time
|
Best GA
|
Average GA (for 5
runs)
|
Number of Generations
|
GA Run Time (single
run)
|
|
8
|
74, 73.8
|
2 minutes
|
74
|
73.68
|
5
|
2 minutes
|
|
10
|
75.2, 75
|
13 minutes
|
75.2
|
74.96
|
5
|
3 minutes
|
|
12
|
77.2, 77
|
47 minutes
|
77
|
76.92
|
10
|
5 minutes
|
|
14
|
79, 78.8
|
3 hours
|
79
|
78.2
|
10
|
5.5 minutes
|
|
16
|
79.2, 79
|
6 hours
|
79.2
|
78.48
|
15
|
8 minutes
|
|
18
|
79.4, 79.2
|
1.5 days
|
79.4
|
78.92
|
20
|
11 minutes
|
Table 4:
Number of Generations to Convergence
The following
observations can be made:
-
In every
case, GA-based FS was able to find the optimal or sub-optimal
values found by exhaustive search. However, the GA took much less
time to find the same optimal or near-optimal values returned by
the exhaustive search. With only 8 features, the run times for
both exhaustive and GA searches are identical. However, for 18
features, the run time for the exhaustive search was 1.5 days
compared to 11 minutes for the GA.
-
As the
number of features increases, the number of generations required
finding optimal or sub-optimal values increases as well.
Figure 10
below displays the relationship between the numbers of generations
needed to reach
optimal or
sub-optimal values with a GA, and the number of features in the
original set. The tiny triangles represent actual data from table 4
(above). There are also two curves in figure 10. The solid line
represents a best-fit piece-wise linear curve that fits to, and
extrapolates, the data points. The extrapolated segment of this
curve (beyond 18 features) represents the most optimistic projection
of GA run time duration. The dotted line represents an
exponential curve that fits to, and extrapolates, the same data
points. The extrapolated segment of this curve (again, beyond 18
features) represents the most pessimistic projection of GA run time
duration. The reason for use of extrapolation is the obviously
impossible amount of time required to run exhaustive searches of
large feature spaces using a single-processor computer. In any case,
one can safely conclude that the time needed for a GA-based search
is bound, on the lower side by the (optimistic) best-fit curve, and
on the upper side, by the (pessimistic) exponential curve.

Figure 10:
Number of Generations to Convergence as
a Function of Number of Features
Using
exponential extrapolation, the number of generations expected for 60
features is 10585, while it is only 89 for linear extrapolation. The
true value should be something in between. If we assume that the
true value is midway between 89 and 10585 (which is 5337), then
running the GA will be computationally expensive. In such cases,
using methods of parallel GA, such as DVeGA (Moser, 1999), becomes
necessary. Also, the authors are currently involved in the
construction of a 10-processor dedicated Linux-PC cluster, which
allows for genuine implementations of parallel GA architectures,
including the one just mentioned. This is important, since the
relative value of GA-based techniques is most pronounced when the
search (e.g. feature) spaces involved are quite large.
We conclude that GA-based feature selection is a reliable method of
locating optimal or near-optimal feature sub-sets. These techniques
also save time, relative to exhaustive searches. However, their
effective use in large feature spaces is dependant upon the
invention of specialized feature selection/weighting methods (e.g.,
DveGa) or/and the availability of parallel processors.
Page 1,
Page 2, Page 3,
Page 4
| 
![]()
