|
Fast and Robust GA-Based Ellipse Detection
J. Yao and N. Kharma
Keywords
Genetic Algorithms, clustering, Sharing GA, Randomized Hough
Transform, shape detection, ellipse detection.
1. Introduction
In this paper, we propose a novel Multi-Population Genetic
Algorithm (MPGA) for accurate and efficient detection of multiple imperfect
(e.g. partial) ellipses in noisy images. This capability that the algorithm
provides is genuinely useful for many real-world image processing applications,
such as: object detection and pattern recognition, scene characterization and
event detection.
Rather than evolving a single population, as in traditional
Genetic Algorithms, we evolve a number of subpopulations. These subpopulations
simultaneously seek all potential optima, resulting in a dramatic increase in
the GA's ability to detect multiple ellipses (compared, for example, to the
Sharing GA technique SGA) [10]). Indeed, not only is the leading edge of
GA-based ellipse detection techniques advanced, but also the MPGA's detection
ability and computational efficiency are superior to those of the widely-used
Randomized Hough Transform (RHT) [8].
Our MPGA algorithm employs both evolution and clustering to
detect ellipses. In addition, the algorithm uses two complementary measures of
fitness and specially designed forms of crossover and mutation. This results in
a robust algorithm that performs very well on images with multiple ellipses,
imperfect ellipses, and in the presence of noise. These are additional
advantages that our algorithm has over other techniques such as RHT and SGA,
whose performance degrade considerably in the presence of multiple ellipses
or/and noise.
Section 2 provides the reader with some necessary background
material, and discusses a number of related research articles. In section 3,
the new algorithm is explained in detail. Section 4 presents and analyzes the
experimental results; it compares the performance of MPGA with both RHT and
SGA. Section 5 concludes the paper and summarizes planned future work.
2. Background
In the literature, the Hough Transform (HT) is one of the most
widely used techniques for location of various geometric shapes [8]. Basically,
the Standard Hough Transform (SHT) represents a geometric shape by a set of
appropriate parameters. For example, a circle could be represented by the
coordinates of its centre and radius, hence 3 parameters. In an image, each
foreground (e.g. black) pixel is mapped onto the space formed by the
parameters. However, since we are dealing with digital computers, this
parameter space is quantized into a number of bins. Peaks in the bins provide
the best indication of where shapes (in the original image) may be. Obviously,
since the parameters are quantized into discrete bins, the intervals of the
bins directly affect the accuracy of the results and the computational effort
required to obtain them. For fine quantization of the space, the algorithm
returns more accurate results, while suffering from large memory loads (for
bins), and expensive computation - especially in highdimensional feature
spaces. Hence, the SHT is most commonly used in 2 or 3-dimensional feature
spaces and is unsuitable for higher dimensional spaces. Ellipses, for example,
are five-dimensional. More efficient HT based methods have been developed [5,
7, 9]. They improve efficiency by (a) exploiting the symmetrical nature of some
shapes, and (b) utilizing intelligent means of dimensionality reduction.
Nevertheless, both computational complexity and memory load remain a serious
problem.
One of the fastest and most widely used variant of the Hough
Transform is the Randomized Hough Transform proposed by Xu et al. [18].
It improves HT with respect to both memory load and speed. The idea is to
randomly pick n pixels from the image (n depends on the
dimensionality of the geometric shape to be extracted), and then solve n
parallel equations to get a set of parameter values (representing a
"candidate shape"). The target image is then tested to see if there
are actual pixels that match or approximate the candidate shape. If there are
such pixels, then a score is assigned to the bin corresponding to the candidate
shape. Finally, after this operation is repeated for many candidate shapes, the
candidate with the highest score represents the best approximation of an actual
shape in the target image. The actual shape in the image can then be extracted.
McLaughlin's work [13] shows that RHT produces improvements in accuracy and
computational complexity, as well as a reduction in the number of false
positives (non-existent ellipses), when compared with the original HT and
number of its improved variants.
The Genetic Algorithm (GA) is another interesting way for
extracting ellipses. As early as 1992, Roth et al. [15] proposed a way
of extracting geometric shapes using Genetic Algorithms [15]. Since then, a
number of GA-based techniques have been developed for the purpose of detecting
specific geometric shapes such as straight lines [2], ellipses [10, 11, 12,
14], and polygons [10, 11, 12].
Procter et al. [14] made an interesting comparison
between GA and RHT. These two techniques have the following features in common:
-
Representation of geometric shapes using minimal sets of parameters.
-
Random sampling of image data.
-
Sequential extraction of multiple shapes.
Their experiments clearly demonstrate that GA-based techniques
return superior results to those produced by RHT methods when a high level of
noise is present in the image but RHT methods are more attractive for
relatively noise-fee images. Indeed, for an elliptical curve with length L
pixels in an image with a total of A pixels, the probability of locating this
curve from a single sample is:

Where n is the dimensionality of the geometric shape; and C
is the unordered selection of y pixels from the complete pixel set X.
With the same probability P for each sampling and the
same number of samples (say N), RHT gets N independent chances of
detection when exploring the search space, sequentially. In contrast, a GA
explores the search space in parallel (using a population with size M),
while guiding the search towards areas of promise within N/M generations.
Moreover, unlike the RHT, which locates peaks in the fitness surface after an
exhaustive search of the space, a GA generates improved offspring from
individuals, mainly through crossover and mutation. Hence, the RHT executes a
blind sequential search, while a GA is able to search the space iteratively
(while receiving feedback) and in parallel. Hence, GA based algorithms have
inherent strengths which, if properly utilized, can make them a better approach
than any RHT based algorithm.
Of course, if there is only a small amount of noise in the image
( A L +/-= and 1 +/-= P ), RHT will converge quickly, since each
sampling has a high probability of locating the target shape. However, in cases
where there is a lot ofnoise, multiple ellipses, or partial ellipses with some
noise, RHT tends to overlook small elliptical curves, since in those cases, C^nl
decreases dramatically with a small L, which leads to an extremely small P.
In this case, a GA based algorithm is likely to converge faster, and exhibit
more robustness as well as accuracy than the RHT. This conclusion matches the
experimental results of Procter et al. [14] and is further supported by
our own experimental data (see section 4).
With GA-based shape detection methods, a straightforward
implementation gives us a fitness function that lacks the flexibility necessary
for the detection of multiple ellipses in an image. A fitness function with a
single term, which only reflects how well a candidate shape matches an
idealized ellipse, will drive the whole population towards a single global
optimum. Hence, in the presence of multiple optima (ellipses), the final winner
is obtained randomly. Moreover, when there are both perfect and imperfect
ellipses, the latter, being locally optimum, will most likely be replaced with
better (more perfect) individuals during evolution, and eventually ignored.
A possible and intuitive solution is to extract shapes
sequentially, as in [2, 14 and 15]. This entails removing detected shapes from
the image, one at a time, (sequentially), and iterating, until there are no
more shapes that the program is able to detect in the image. It is clear that
this approach involves a high degree of redundancy and, as such, is
computationally inefficient.
Lutton et al. [10] improve the simple GA by using a Sharing
technique, first introduced by Goldberg et al. [3] in 1987. This technique aims
to maintain the diversity of the population by scaling up the fitnesses of
local optima within the population (so that they would stand out). The basic
idea is that "raw" fitness fi of every individual is scaled up/down
using a sharing function sh(dij) in the following manner:

dij is the phonotypical distance between two individuals i and
j. N is the total number of individuals in the population. The sharing
function, sh(dij), is further defined as:

Here sigma share
is a constant distance, intended to separate different subpopulations, and
alpha
is another constant used to configure the shape of the sharing function (and
usually set to 1).
In this scheme, fitness is shared among similar individuals, and
hence the fitnesses of those individuals with many neighbors are reduced. Thus,
population diversity is maintained by encouraging the exploration of less
crowded regions of the fitness surface.
Unfortunately, Goldberg's implement-ation is based on the
assumption that the neighborhoods of local optima are less crowded (with
individuals) than the neighborhood of the global optimum and that, therefore,
the fitnesses of local optima will be enhanced by sharing. This assumption is
not valid for our application, as imperfect ellipses may attract many neighbors
with a high probability P, as long as they contain a sufficiently large number
of pixels (refer to equation (1)). This will deflect the search from
exploring potentially promising areas, and will, often, result in missed
ellipses.

Fig. 1 provides a concrete example. After running the Sharing
GA, to convergence, with a population size of 100, the individual (candidate
ellipse) at the centre of the densest subpopulation of individuals, is
represented in Fig. 1 (b) by an overlaid grey ellipse. Since the left ellipse
is larger (in terms of pixels) than the right one, it is natural that the left
ellipse will attract more individuals (ellipse candidates) around it. However,
the ellipse on the left corresponds to a local optimum (with sub-optimal
fitness), while the right perfectly formed ellipse corresponds to the global
maximum (with the highest fitness). Hence, if the sharing function is applied:
the fitness of the sub-optimal individual, will be shared with the rest of its
dense subpopulation, and on the other hand, the fitness of the optimal
individual will be shared with the rest of its less dense subpopulation. This
will result in a global optimum (right ellipse), which is even more pronounced
relative to the local optimum (right ellipse) than the case was before the
sharing function was applied. Therefore, sharing in this example defeats the
purpose of the exercise.
Furthermore, Smith et al. [16] highlighted the fact that the
computation of the distance of an individual to any/all other individuals in a
population has a time complexity of O(N^2), where N is the size of the
population [16].

The new shared fitness becomes:
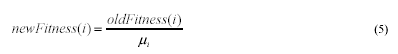
new Fitness reflects the relative fitness of individual i with
respect to its own subpopulation. N is the number of individuals in the
subpopulation and sh(dik) is defined in the same manner as sh(dij)
above - see equation (3).
However, the new algorithm still operates under the assumption
that local optima reside in less crowded neighborhoods than the global optimum,
which means it still suffers from the same fault as the older algorithm.
Indeed, our own experiments show that, when multiple ellipses or/and high noise
are present in a target image, the Sharing GA fails badly (see section 4).
To overcome the various problems discussed above, with both RHT
and SGA, we developed and tested a new multiple-population GA, with the
following key features:
-
Parallel evolution of multiple subpopulations each focused on a potential
elliptical pattern in the image;
-
Clustering is used to effectively create and maintain the multiple
subpopulations;
-
Use of two fitness terms to enhance the overall fitness of local optima in an
effective manner;
-
Customized crossover and mutation operators to take advantage of specialized
domain-knowledge;
Experiments show that this algorithm works well for multiple
ellipses, imperfect ellipses, and high noise.
Page 1, Page 2, Page 3,
Page 4
|

![]()
